Contents
Outline
We consider to turn RC pressure tunnel with the uniform circular cross section into a multiple cyclinder model with thick wall in the state of the plane strain.
In this case, it is not necessary to consider the shearing strain and stress because of zero of those values.
Concept for making a model is indicated below.
- The pressure tunnel has the uniform circular cross section and it is a RC structure.
- The area of a model submitted to the internal water pressure includes the RC structure and the bedrock.
- The concrete submitted to the internal water pressure does not transmit the circumferential tensile stress because of the crack occurrence.
- The external water pressure is act on the outer surface of the concrete, and the bedrock area is not included in the model.
- Since only compressive stress is act to the RC structure submitted to the external water pressure, it seems that the concrete and re-bar have complete elastic bodies.
- The uniform temperature change in the RC structure is considered and the temperature change in the bedrock is not considered because of simplification of a model.
- Since the cover of the re-bar is large comparatively, the cover is considered in the model.
Basic theory is created refering to the text of ''Theory of Elasticity, Chapter 13 Thermal Stress'' by Timoshenko and Goodier.
Basic equations
Complete elastic body
Since it is not necessary to consider the shearing strain and stress in the uniform pressure and the uniform circular cross section,
general expressions of the stress-strain relationship can be indicated below.
\begin{equation}
\begin{cases}
\epsilon_r -\alpha T=\cfrac{1}{E}\{\sigma_r-\nu(\sigma_{\theta}+\sigma_z)\} \\
\epsilon_{\theta}-\alpha T=\cfrac{1}{E}\{\sigma_{\theta}-\nu(\sigma_z+\sigma_r)\} \\
\epsilon_z -\alpha T=\cfrac{1}{E}\{\sigma_z-\nu(\sigma_r+\sigma_{\theta})\}
\end{cases}
\end{equation}
where,
| $r$ | Radial direction | | $E$ | Elastic modulus of the material |
| $\theta$ | Circumferential direction | | $\nu$ | Poisson's ratio of the material |
| $z$ | Logitudinal direction | | $\alpha$ | Coefficient of the thermal expansion |
| $\sigma$ | Normal stress | | $T$ | Temperature change |
| $\epsilon$ | Normal strain | | | |
In the state of the plane strain, $\epsilon_z=0$ . Then,
\begin{equation}
\begin{cases}
\sigma_z=\nu(\sigma_r+\sigma_{\theta})-E\alpha T \\
\epsilon_r -\alpha T=\cfrac{1}{E}\{(1-\nu^2)\sigma_r-\nu(1+\nu)\sigma_{\theta}\} \\
\epsilon_{\theta}-\alpha T=\cfrac{1}{E}\{(1-\nu^2)\sigma_{\theta}-\nu(1+\nu)\sigma_r\}
\end{cases}
\end{equation}
\begin{equation}
\begin{cases}
\sigma_r =\cfrac{E}{(1+\nu)(1-2\nu)}\{(1-\nu)\epsilon_r+\nu\epsilon_{\theta}-(1+\nu)\alpha T\} \\
\sigma_{\theta}=\cfrac{E}{(1+\nu)(1-2\nu)}\{\nu\epsilon_r+(1-\nu)\epsilon_{\theta}-(1+\nu)\alpha T\}
\end{cases}
\end{equation}
The strain-displacement relationship (compatibility equations) can be expressed below, where $u$ means the displacement in the radial direction.
\begin{equation}
\epsilon_r=\cfrac{du}{dr} \qquad \epsilon_{\theta}=\cfrac{u}{r}
\end{equation}
The differential equations of equilibrium in the thick wall circular cylinder becomes shown below.
\begin{equation}
\cfrac{d\sigma_r}{dr}+\cfrac{\sigma_r-\sigma_{\theta}}{r}=0
\end{equation}
(Reference)
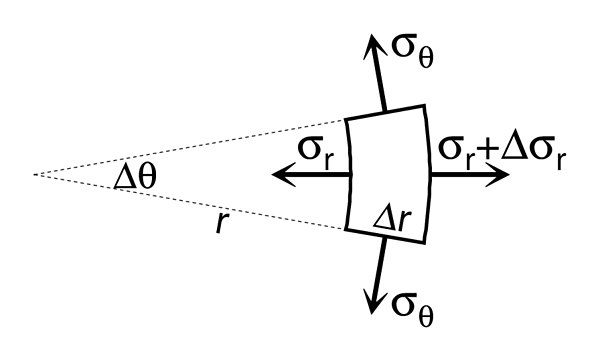
We can obtain following equation from equilibrium of small element,
\begin{equation*}
r\Delta\theta\cdot\sigma_r+2 dr\cdot\sigma_{\theta}\sin\left(\frac{\Delta\theta}{2}\right)=(r+dr) \Delta\theta (\sigma_r+d\sigma_r)
\end{equation*}
From above, the differential equation shown below can be derived using the approximation of $\sin(\Delta\theta/2) \doteqdot \Delta\theta/2$ , eliminating $\Delta\theta$ from both side and neglecting the small terms.
\begin{equation*}
\cfrac{d\sigma_r}{dr}+\cfrac{\sigma_r-\sigma_{\theta}}{r}=0
\end{equation*}
Therefore,
\begin{equation}
\cfrac{d\sigma_r}{dr}+\cfrac{\sigma_r-\sigma_{\theta}}{r}
=\cfrac{E(1-\nu)}{(1+\nu)(1-2\nu)}\left\{\cfrac{d^2
u}{dr^2}+\cfrac{1}{r}\cfrac{du}{dr}-\cfrac{u}{r^2}-\cfrac{(1+\nu)}{(1-\nu)}\cdot\alpha\cfrac{dT}{dr}\right\}=0
\end{equation}
\begin{equation}
\cfrac{d^2 u}{dr^2}+\cfrac{1}{r}\cfrac{du}{dr}-\cfrac{u}{r^2}=\cfrac{(1+\nu)}{(1-\nu)}\cdot\alpha\cfrac{dT}{dr}
\qquad\rightarrow\qquad
\cfrac{d}{dr}\left[\cfrac{1}{r}\cfrac{d(ru)}{dr}\right]=\cfrac{(1+\nu)}
{(1-\nu)}\cdot\alpha\cfrac{dT}{dr}
\end{equation}
where,
\begin{align}
\cfrac{d}{dr}\left[\cfrac{1}{r}\cfrac{d(ru)}{dr}\right]=0
\quad \rightarrow\quad \text{general solution}\quad u=C_1\cdot r+\cfrac{C_2}{r} \\
\cfrac{d}{dr}\left[\cfrac{1}{r}\cfrac{d(ru)}{dr}\right]=\cfrac{(1+\nu)}{(1-\nu)}\cdot\alpha\cfrac{dT}{dr}
\quad
\rightarrow\quad \text{particular solution}\quad
u=\cfrac{1+\nu}{1-\nu}\cdot\alpha\cfrac{1}{r}\int_a^r T r dr
\end{align}
From above, following equations related to the displacement and stress can be obtained.
In the following equations, $r$ means the coordinate in the radial direction, and $a$ means the radial coordinate of the smaller boundary value in each material.
\begin{equation}
\begin{cases}
\displaystyle u = \cfrac{1+\nu}{1-\nu}\cdot
\alpha\cfrac{1}{r}\int_a^r T r dr+C_1\cdot r+\cfrac{C_2}{r} \\
\displaystyle \sigma_r =-\cfrac{\alpha E}{1-\nu}\cdot
\cfrac{1}{r^2}\int_a^r T r dr+\cfrac{E}{(1+\nu)(1-2\nu)}\cdot
C_1-\cfrac{E}{(1+\nu)}\cfrac{C_2}{r^2} \\
\displaystyle \sigma_{\theta}= \cfrac{\alpha E}{1-\nu}\cdot
\cfrac{1}{r^2}\int_a^r T r dr-\cfrac{\alpha E
T}{1-\nu}+\cfrac{E}{(1+\nu)(1-2\nu)}\cdot
C_1+\cfrac{E}{(1+\nu)}\cfrac{C_2}{r^2} \\
\displaystyle \sigma_z =-\cfrac{\alpha E T}{1-\nu}+\cfrac{2\nu
E}{(1+\nu)(1-2\nu)}\cdot C_1
\end{cases}
\end{equation}
No-tension material in the circumferential direction
We consider the concrete submitted the internal water pressure which cannot transmit the circumferential tensile stress, and find the basic equation of that behavior.
In the equation of equilibrium, following equation can be obtain using the condition of $\sigma_{\theta}=0$ .
\begin{equation}
\cfrac{d\sigma_r}{dr}+\cfrac{\sigma_r}{r}=0
\end{equation}
Since the no-tension material can seem a uniaxial material, we can assume the Poisson's ratio is equal to zero ( $\nu=0$ ).
So, following equations can be obtained using the stress-strain relationship.
\begin{equation}
\sigma_r=E\epsilon_r-E\alpha T \quad\rightarrow\quad
\sigma_r=E\cfrac{du}{dr}-E\alpha T \quad
\left(\epsilon_r=\cfrac{du}{dr}\right)
\end{equation}
\begin{equation}
\cfrac{d\sigma_r}{dr}+\cfrac{\sigma_r}{r}=E\left\{\cfrac{d^2 u}{dr^2}+\cfrac{1}{r}\cfrac{du}{dr}-\alpha\left(\cfrac{dT}{dr}+\cfrac{T}{r}\right)\right\}=0
\end{equation}
Next, we can find a general solution and a particular solution of the differential equation as follow.
\begin{align}
\cfrac{d^2 u}{dr^2}+\cfrac{1}{r}\cfrac{du}{dr}=0
\quad \rightarrow\quad \text{general solution}\quad u=C_1+C_2\ln(r) \\
\cfrac{d^2 u}{dr^2}+\cfrac{1}{r}\cfrac{du}{dr}-\alpha\left(\cfrac{dT}{dr}+\cfrac{T}{r}\right)
\quad
\rightarrow\quad \text{particular solution}\quad u=\alpha\int_a^r T dr
\end{align}
From above, we can find the displacement and stress as follows.
Regarding the sequence of $C_1$ and $C_2$ , it is considered that diagonal members in the simultaneous equations don't become zero.
And in the following equations, $r$ means the coordinate in the radial direction, and $a$ means the radial coordinate of the smaller boundary value in each material.
\begin{equation}
\begin{cases}
\displaystyle u=C_1+C_2\ln(r)+\alpha\int_a^r T dr \\
\displaystyle \sigma_r=E\cfrac{C_2}{r}
\end{cases}
\end{equation}
Application of the basic equation to each material
We apply the basic equations to each materials which compose the model.
And we confirm the following assumptions.
- The bedrock has the complete elastic body.
- The re-bar has the complete elastic body and it can transmit the stresses in the radial and circumferential direction and also tensile and compressive stresses.
- The concrete submitted to the internal pressure seems the no-tension material in the circumferential direction.
- The concrete submitted to the external pressure has the complete elastic body.
- The normal stress in the longitudinal direction $\sigma_z$ is not considered because it can be obtained as a result of the calculation of other items.
- The temperature change is considered only in the RC structure and the value of it has uniform distribution in the RC structure. The temperature change in the bedrock is not considered.
Bedrock
The basic equation for the bedrock is shown below under the condition of complete elastic body and no temperature change.
\begin{equation}
\begin{cases}
\displaystyle u_g =C_{g1}\cdot r+\cfrac{C_{g2}}{r} \\
\displaystyle \sigma_{rg} =\cfrac{E_g}{(1+\nu_g)(1-2\nu_g)}\cdot C_{g1}-\cfrac{E_g}{(1+\nu_g)}\cfrac{C_{g2}}{r^2} \\
\displaystyle \sigma_{\theta g}=\cfrac{E_g}{(1+\nu_g)(1-2\nu_g)}\cdot C_{g1}+\cfrac{E_g}{(1+\nu_g)}\cfrac{C_{g2}}{r^2}
\end{cases}
\end{equation}
Re-bar
The basic equation for the re-bar is shown below under the condition of complete elastic body and unidorm temperature change.
\begin{equation}
\begin{cases}
\displaystyle \cfrac{1+\nu_s}{1-\nu_s}\cdot \alpha_s\cfrac{1}{r}\int_a^r T r dr=\cfrac{1+\nu_s}{1-\nu_s}\cdot \alpha_s T \cfrac{r^2-a^2}{2r} \\
\displaystyle \cfrac{\alpha_s E_s}{1-\nu_s}\cdot \cfrac{1}{r^2}\int_a^r T r dr=-\cfrac{E_s \alpha_s T}{1-\nu}\cdot \cfrac{r^2-a^2}{2r^2} \\
\displaystyle \cfrac{\alpha_s E_s}{1-\nu_s}\cdot \cfrac{1}{r^2}\int_a^r T r dr-\cfrac{\alpha_s E_s T}{1-\nu}=-\cfrac{E_s \alpha_s T}{1-\nu}\cdot \cfrac{r^2+a^2}{2r^2}
\end{cases}
\end{equation}
Thus,
\begin{equation}
\begin{cases}
\displaystyle u_s = \cfrac{1+\nu_s}{1-\nu_s}\cdot \alpha_s T \cfrac{r^2-a^2}{2r}+C_{s1}\cdot r+\cfrac{C_{s2}}{r} \\
\displaystyle \sigma_{rs} =-\cfrac{E_s \alpha_s T}{1-\nu}\cdot
\cfrac{r^2-a^2}{2r^2}+\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)}\cdot
C_{s1}-\cfrac{E_s}{(1+\nu_s)}\cfrac{C_{s2}}{r^2} \\
\displaystyle \sigma_{\theta s}=-\cfrac{E_s \alpha_s T}{1-\nu}\cdot
\cfrac{r^2+a^2}{2r^2}+\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)}\cdot
C_{s1}+\cfrac{E_s}{(1+\nu_s)}\cfrac{C_{s2}}{r^2}
\end{cases}
\end{equation}
Concrete submitted to the internal water pressure (no-tension material)
The basic equation for the concrete is shown below under the condition of no-tension material and unidorm temperature change.
\begin{equation}
\alpha_c\int_a^r T dr=\alpha_c T(r-a)
\end{equation}
Thus,
\begin{equation}
\begin{cases}
\displaystyle u_c=C_{c1}+C_{c2}\ln(r)+\alpha_c T(r-a) \\
\displaystyle \sigma_{rc}=E_c\cfrac{C_{c2}}{r} \\
\displaystyle \sigma_{\theta c}=0
\end{cases}
\end{equation}
Concrete submitted to the external water pressure (complete elastic body)
The basic equation for the concrete is shown below under the condition of complete elastic body and unidorm temperature change.
\begin{equation}
\begin{cases}
\displaystyle u_c = \cfrac{1+\nu_c}{1-\nu_c}\cdot \alpha_c T
\cfrac{r^2-a^2}{2r}+C_{c1}\cdot r+\cfrac{C_{c2}}{r} \\
\displaystyle \sigma_{rc} =-\cfrac{E_c \alpha_c T}{1-\nu}\cdot
\cfrac{r^2-a^2}{2r^2}+\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)}\cdot
C_{c1}-\cfrac{E_c}{(1+\nu_c)}\cfrac{C_{c2}}{r^2} \\
\displaystyle \sigma_{\theta s}=-\cfrac{E_c \alpha_c T}{1-\nu}\cdot
\cfrac{r^2+a^2}{2r^2}+\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)}\cdot
C_{c1}+\cfrac{E_c}{(1+\nu_c)}\cfrac{C_{c2}}{r^2}
\end{cases}
\end{equation}
Assembly of the simultaneous equations
We assemble the simultaneous equations applying the boundary conditions at the joints of the materials.
If we solve that simultaneous equations, we can know the undetermined coefficients and evaluate the displacement and stress of the structure.
- Model submitted to the internal water pressure
Loads considered are the internal water pressure (positive: outer direction) and uniform temperature change in the RC structure (positive: temperature increase).
The concrete seems the no-tension material.
- Model submitted to the external water pressure
Loads considered are the external water pressure which is act on the the outer surface of concrete (positive: inner direction) and uniform temperature change in the RC structure (positive: temperature increase).
The concrete seems the complete elastic material.
If the temperature decrease has large effect, the tensile stress may be observed in the concrete body.
In this case, it shall be checked the value of tensile stress exceeds the tensile strength of the concrete or not.
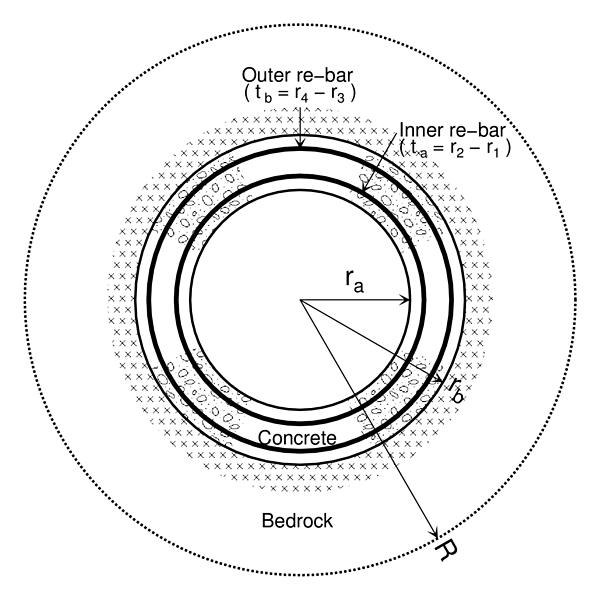 |
| Model of RC Presuure Tunnel for Analysis |
|---|
| Loading condition for the each model |
|---|
| Model | Internal Pressure Model | External Pressure Model |
|---|
| Load model |
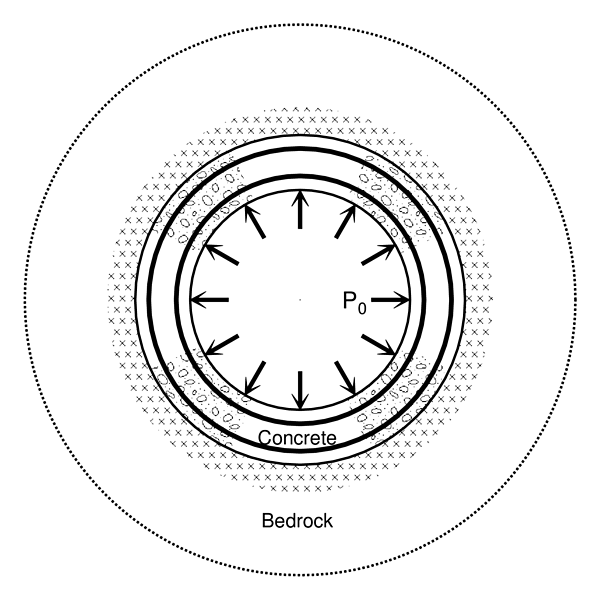 |
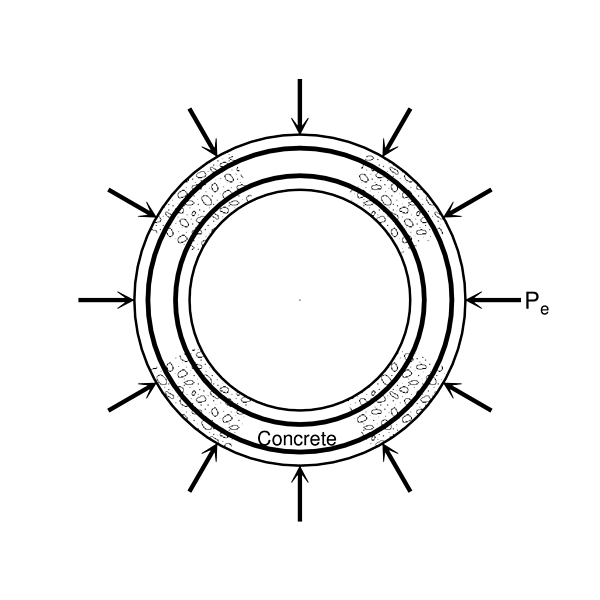 |
| Concrete: No-tension body | Concrete: Linear elastic body |
| Bed rock is included. | Bed rock is not included. |
| Loads | Internal pressure $P_0$ | External pressure $P_e$ |
| Temperature change | Temperature change |
| Re-bar | Double or Single | Double or Single |
| n *) | Double: 12th, Single: 8th | Double: 10th, Single: 6th |
| *) n is the dimension of linear equations. |
Single re-bar section submitted to the internal water pressure
| Row | Location | Condition | Coefficient | Type of unknown |
|---|
| 1 | $r=R$ | Zero displacement at the outer edge of the bedrock | $C_{g1}$ | $C_1$ for the bedrock |
| 2 | $r=r_b$ | Continuity of the stress value at the boundary of the bedrock and concrete | $C_{g2}$ | $C_2$ for the bedrock |
| 3 | $r=r_b$ | Continuity of the displacement at the boundary of the bedrock and the concrete | $C_{co1}$ | $C_1$ for the concrete |
| 4 | $r=r_2$ | Continuity of the stress value at the concrete and outer surface of the re-bar | $C_{co2}$ | $C_2$ for the concrete |
| 5 | $r=r_2$ | Continuity of the displacement at the concrete and outer surface of the re-bar | $C_{s1}$ | $C_1$ for the re-bar |
| 6 | $r=r_1$ | Continuity of the stress value at the concrete and inner surface of the re-bar | $C_{s2}$ | $C_2$ for the re-bar |
| 7 | $r=r_1$ | Continuity of the displacement at the concrete and inner surface of the re-bar | $C_{ci1}$ | $C_1$ for the concrete |
| 8 | $r=r_a$ | The stress value at inner surface of the concrete is equal to the internal pressure $P_0$ | $C_{ci2}$ | $C_2$ for the concrete |
\begin{equation}
\begin{bmatrix}
a_{1,1} & a_{1,2} & 0 & 0 & 0 & 0 & 0 & 0 \\
a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4} & 0 & 0 & 0 & 0 \\
a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} & 0 & 0 & 0 & 0 \\
0 & 0 & a_{4,3} & a_{4,4} & a_{4,5} & a_{4,6} & 0 & 0 \\
0 & 0 & a_{5,3} & a_{5,4} & a_{5,5} & a_{5,6} & 0 & 0 \\
0 & 0 & 0 & 0 & a_{6,5} & a_{6,6} & a_{6,7} & a_{6,8} \\
0 & 0 & 0 & 0 & a_{7,5} & a_{7,6} & a_{7,7} & a_{7,8} \\
0 & 0 & 0 & 0 & 0 & 0 & a_{8,7} & a_{8,8} \\
\end{bmatrix}
\begin{Bmatrix}
C_{g1} \\ C_{g2} \\ C_{co1} \\ C_{co2} \\ C_{s1} \\ C_{s2} \\ C_{ci1} \\
C_{ci2} \\
\end{Bmatrix}
=
\begin{Bmatrix}
0 \\
0 \\
\alpha_c T(r_b-r_2) \\
-\frac{E_s \alpha_s T}{1-\nu_s}\cdot\frac{r_2{}^2-r_1{}^2}{2\cdot
r_2{}^2} \\
\frac{1+\nu_s}{1-\nu_s}\alpha_s T \cdot\frac{r_2{}^2-r_1{}^2}{2\cdot
r_2} \\
0 \\
\alpha_c T(r_1-r_a) \\
-P_0 \\
\end{Bmatrix}
\end{equation}
\begin{align*}
&a_{1,1}=R &~&a_{1,2}=\cfrac{1}{R} &~& &~& \\
&a_{2,1}=\cfrac{E_g}{(1+\nu_g)(1-2\nu_g)} & &a_{2,2}=-\cfrac{E_g}{1+\nu_g}\cdot\cfrac{1}{r_b{}^2} & &a_{2,3}=0 & &a_{2,4}=\cfrac{E_c}{r_b} \\
&a_{3,1}=r_b & &a_{3,2}=\cfrac{1}{r_b} & &a_{3,3}=-1 & &a_{3,4}=-\ln(r_b) \\
&a_{4,3}=0 & &a_{4,4}=\cfrac{E_c}{r_2} & &a_{4,5}=-\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{4,6}=\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_2{}^2} \\
&a_{5,3}=1 & &a_{5,4}=\ln(r_2) & &a_{5,5}=-r_2 & &a_{5,6}=-\cfrac{1}{r_2} \\
&a_{6,5}=\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{6,6}=-\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_1{}^2} & &a_{6,7}=0 & &a_{6,8}=-\cfrac{E_c}{r_1} \\
&a_{7,5}=r_1 & &a_{7,6}=\cfrac{1}{r_1} & &a_{7,7}=-1 & &a_{7,8}=-\ln(r_1) \\
&a_{8,7}=0 & &a_{8,8}=\cfrac{E_c}{r_a} & & & & \\
\end{align*}
Double re-bar section submitted to the internal water pressure
| Row | Location | Condition | Coefficient | Type of unknown |
|---|
| 1 | $r=R$ | Zero displacement at the outer edge of the bedrock | $C_{g1}$ | $C_1$ for the bedrock |
| 2 | $r=r_b$ | Continuity of the stress value at the boundary of the bedrock and the concrete | $C_{g2}$ | $C_2$ for the bedrock |
| 3 | $r=r_b$ | Continuity of the displacement at the boundary of the bedrock and the concrete | $C_{co1}$ | $C_1$ for the concrete |
| 4 | $r=r_4$ | Continuity of the stress value at the concrete and the outer surface of outer re-bar | $C_{co2}$ | $C_2$ for the concrete |
| 5 | $r=r_4$ | Continuity of the displacement at the concrete and the outer surface of outer re-bar | $C_{so1}$ | $C_1$ for the outer re-bar |
| 6 | $r=r_3$ | Continuity of the stress value at the concrete and the inner surface of outer re-bar | $C_{so2}$ | $C_2$ for the outer re-bar |
| 7 | $r=r_3$ | Continuity of the displacement at the concrete and the inner surface of outer re-bar | $C_{cm1}$ | $C_1$ for the concrete |
| 8 | $r=r_2$ | Continuity of the stress value at the concrete and the outer surface of inner re-bar | $C_{cm2}$ | $C_2$ for the concrete |
| 9 | $r=r_2$ | Continuity of the displacement at the concrete and the outer surface of inner re-bar | $C_{si1}$ | $C_1$ for the inner re-bar |
| 10 | $r=r_1$ | Continuity of the stress value at the concrete and the inner surface of inner re-bar | $C_{si2}$ | $C_2$ for the inner re-bar |
| 11 | $r=r_1$ | Continuity of the displacement at the concrete and the inner surface of inner re-bar | $C_{ci}$ | $C_1$ for the concrete |
| 12 | $r=r_a$ | The stress value at inner surface of the concrete is equal to the internal pressure $P_0$ | $C_{ci}$ | $C_2$ for the concrete |
\begin{equation}
\begin{bmatrix}
a_{1,1} & a_{1,2} & 0 & 0 & 0 & 0 & \cdots & 0 & 0 \\
a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4} & 0 & 0 & \cdots & 0 & 0 \\
a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & a_{4,3} & a_{4,4} & a_{4,5} & a_{4,6} & \cdots & 0 & 0 \\
0 & 0 & a_{5,3} & a_{5,4} & a_{5,5} & a_{5,6} & \cdots & 0 & 0 \\
0 & 0 & 0 & 0 & a_{6,5} & a_{6,6} & \cdots & 0 & 0 \\
0 & 0 & 0 & 0 & a_{7,5} & a_{7,6} & \cdots & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & \cdots & a_{10,11} & a_{10,12} \\
0 & 0 & 0 & 0 & 0 & 0 & \cdots & a_{11,11} & a_{11,12} \\
0 & 0 & 0 & 0 & 0 & 0 & \cdots & a_{12,11} & a_{12,12} \\
\end{bmatrix}
\begin{Bmatrix}
C_{g1} \\ C_{g2} \\ C_{co1} \\ C_{co2} \\ C_{so1} \\ C_{so2} \\ C_{cm1}
\\ C_{cm2} \\ C_{si1} \\ C_{si2}\\ C_{ci1} \\ C_{ci2} \\
\end{Bmatrix}
=
\begin{Bmatrix}
0 \\
0 \\
\alpha_c T(r_b-r_4) \\
-\frac{E_s \alpha_s T}{1-\nu_s}\cdot\frac{r_4{}^2-r_3{}^2}{2\cdot
r_4{}^2} \\
\frac{1+\nu_s}{1-\nu_s}\alpha_s T \cdot\frac{r_4{}^2-r_3{}^2}{2\cdot
r_4} \\
0 \\
\alpha_c T(r_3-r_2) \\
-\frac{E_s \alpha_s T}{1-\nu_s}\cdot\frac{r_2{}^2-r_1{}^2}{2\cdot
r_2{}^2} \\
\frac{1+\nu_s}{1-\nu_s}\alpha_s T \cdot\frac{r_2{}^2-r_1{}^2}{2\cdot
r_2} \\
0 \\
\alpha_c T(r_1-r_a) \\
-P_0 \\
\end{Bmatrix}
\end{equation}
\begin{align*}
&a_{1,1}=R &~&a_{1,2}=\cfrac{1}{R} &~& &~& \\
&a_{2,1}=\cfrac{E_g}{(1+\nu_g)(1-2\nu_g)} & &a_{2,2}=-\cfrac{E_g}{1+\nu_g}\cdot\cfrac{1}{r_b{}^2} & &a_{2,3}=0 & &a_{2,4}=\cfrac{E_c}{r_b} \\
&a_{3,1}=r_b & &a_{3,2}=\cfrac{1}{r_b} & &a_{3,3}=-1 & &a_{3,4}=-\ln(r_b) \\
&a_{4,3}=0 & &a_{4,4}=\cfrac{E_c}{r_4} & &a_{4,5}=-\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{4,6}=\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_4{}^2} \\
&a_{5,3}=1 & &a_{5,4}=\ln(r_4) & &a_{5,5}=-r_4 & &a_{5,6}=-\cfrac{1}{r_4} \\
&a_{6,5}=\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{6,6}=-\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_3{}^2} & &a_{6,7}=0 & &a_{6,8}=-\cfrac{E_c}{r_3} \\
&a_{7,5}=r_3 & &a_{7,6}=\cfrac{1}{r_3} & &a_{7,7}=-1 & &a_{7,8}=-\ln(r_3) \\
&a_{8,7}=0 & &a_{8,8}=\cfrac{E_c}{r_2} & &a_{8,9}=-\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{8,10}=\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_2{}^2} \\
&a_{9,7}=1 & &a_{9,8}=\ln(r_2) & &a_{9,9}=-r_2 & &a_{9,10}=-\cfrac{1}{r_2} \\
&a_{10,9}=\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{10,10}=-\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_1{}^2} & &a_{10,11}=0 & &a_{10,12}=-\cfrac{E_c}{r_1} \\
&a_{11,9}=r_1 & &a_{11,10}=\cfrac{1}{r_1} & &a_{11,11}=-1 & &a_{11,12}=-\ln(r_1) \\
&a_{12,11}=0 & &a_{12,12}=\cfrac{E_c}{r_a} & & & & \\
\end{align*}
Single re-bar section submitted to the external water pressure
| Row | Location | Condition | Coefficient | Type of unknown |
|---|
| 1 | $r=r_b$ | The stress value at the outer surface of the concrete is equal to the external pressure $P_e$ | $C_{co1}$ | $C_1$ for the concrete |
| 2 | $r=r_2$ | Continuity of the stress value at the boundary of the concrete and outer surface of re-bar | $C_{co2}$ | $C_2$ for the concrete |
| 3 | $r=r_2$ | Continuity of the displacement at the boundary of the concrete and outer surface of re-bar | $C_{s1}$ | $C_1$ for the re-bar |
| 4 | $r=r_1$ | Continuity of the stress value at the boundary of the concrete and inner surface of re-bar | $C_{s2}$ | $C_2$ for the re-bar |
| 5 | $r=r_1$ | Continuity of the displacement at the boundary of the concrete and inner surface of re-bar | $C_{ci1}$ | $C_1$ for the concrete |
| 6 | $r=r_a$ | Zero stress value at the inner surface of the concrete | $C_{ci2}$ | $C_2$ for the concrete |
\begin{equation}
\begin{bmatrix}
a_{1,1} & a_{1,2} & 0 & 0 & 0 & 0 \\
a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4} & 0 & 0 \\
a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} & 0 & 0 \\
0 & 0 & a_{4,3} & a_{4,4} & a_{4,5} & a_{4,6} \\
0 & 0 & a_{5,3} & a_{5,4} & a_{5,5} & a_{5,6} \\
0 & 0 & 0 & 0 & a_{6,5} & a_{6,6} \\
\end{bmatrix}
\begin{Bmatrix}
C_{co1} \\ C_{co2} \\ C_{s1} \\ C_{s2} \\ C_{ci1} \\ C_{ci2} \\
\end{Bmatrix}
=
\begin{Bmatrix}
-P_e \\
-\frac{E_s \alpha_s T}{1-\nu_s}\cdot\frac{r_2{}^2-r_1{}^2}{2\cdot
r_2{}^2} \\
\frac{1+\nu_s}{1-\nu_s}\alpha_s T \cdot\frac{r_2{}^2-r_1{}^2}{2\cdot
r_2} \\
-\frac{E_c \alpha_c T}{1-\nu_c}\cdot\frac{r_1{}^2-r_a{}^2}{2\cdot
r_1{}^2} \\
\frac{1+\nu_c}{1-\nu_c}\alpha_c T \cdot\frac{r_1{}^2-r_a{}^2}{2\cdot
r_1} \\
0 \\
\end{Bmatrix}
\end{equation}
\begin{align*}
&a_{1,1}=\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)} &~&a_{1,2}=-\cfrac{E_c}{1+\nu_c}\cdot\cfrac{1}{r_b{}^2} &~& &~& \\
&a_{2,1}=\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)} & &a_{2,2}=-\cfrac{E_c}{1+\nu_c}\cdot\cfrac{1}{r_2{}^2} & &a_{2,3}=-\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{2,4}=\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_2{}^2} \\
&a_{3,1}=r_2 & &a_{3,2}=\frac{1}{r_2} & &a_{3,3}=-r_2 & &a_{3,4}=-\cfrac{1}{r_2} \\
&a_{4,3}=\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{4,4}=-\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_1{}^2} & &a_{4,5}=-\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)} & &a_{4,6}=\cfrac{E_c}{1+\nu_c}\cdot\cfrac{1}{r_1{}^2} \\
&a_{5,3}=r_1 & &a_{5,4}=\frac{1}{r_1} & &a_{5,5}=-r_1 & &a_{5,6}=-\cfrac{1}{r_1} \\
&a_{6,5}=\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)} &~&a_{6,6}=-\cfrac{E_c}{1+\nu_c}\cdot\cfrac{1}{r_a{}^2} &~& &~& \\
\end{align*}
Double re-bar section submitted to the external water pressure
| Row | Location | Condition | Coefficient | Type of unknown |
|---|
| 1 | $r=r_b$ | The stress value at the outer surface of the concrete is equal to the external pressure $P_e$ | $C_{co1}$ | $C_1$ for the concrete |
| 2 | $r=r_4$ | Continuity of the stress value at the concrete and outer surface of outer re-bar | $C_{co2}$ | $C_2$ for the concrete |
| 3 | $r=r_4$ | Continuity of the displacement at the concrete and outer surface of outer re-bar | $C_{so1}$ | $C_1$ for the outer re-bar |
| 4 | $r=r_3$ | Continuity of the stress value at the concrete and inner surface of outer re-bar | $C_{so2}$ | $C_2$ for the outer re-bar |
| 5 | $r=r_3$ | Continuity of the displacement at the concrete and inner surface of outer re-bar | $C_{cm1}$ | $C_1$ for the concrete |
| 6 | $r=r_2$ | Continuity of the stress value at the concrete and outer surface of inner re-bar | $C_{cm2}$ | $C_2$ for the concrete |
| 7 | $r=r_2$ | Continuity of the displacement at the concrete and outer surface of inner re-bar | $C_{si1}$ | $C_1$ for the inner re-bar |
| 8 | $r=r_1$ | Continuity of the stress value at the concrete and inner surface of inner re-bar | $C_{si2}$ | $C_2$ for the inner re-bar |
| 9 | $r=r_1$ | Continuity of the displacement at the concrete and inner surface of inner re-bar | $C_{ci}$ | $C_1$ for the concrete |
| 10 | $r=r_a$ | Zero stress value at the inner surface of the concrete | $C_{ci}$ | $C_2$ for the concrete |
\begin{equation}
\begin{bmatrix}
a_{1,1} & a_{1,2} & 0 & 0 & \cdots & 0 & 0 \\
a_{2,1} & a_{2,2} & a_{2,3} & a_{2,4} & \cdots & 0 & 0 \\
a_{3,1} & a_{3,2} & a_{3,3} & a_{3,4} & \cdots & 0 & 0 \\
0 & 0 & a_{4,3} & a_{4,4} & \cdots & 0 & 0 \\
0 & 0 & a_{5,3} & a_{5,4} & \cdots & 0 & 0 \\
0 & 0 & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & 0 & 0 & \cdots & a_{8,9} & a_{8,10} \\
0 & 0 & 0 & 0 & \cdots & a_{9,9} & a_{9,10} \\
0 & 0 & 0 & 0 & \cdots & a_{10,9} & a_{10,10} \\
\end{bmatrix}
\begin{Bmatrix}
C_{co1} \\ C_{co2} \\ C_{so1} \\ C_{so2} \\ C_{cm1} \\ C_{cm2} \\
C_{si1} \\ C_{si2}\\ C_{ci1} \\ C_{ci2} \\
\end{Bmatrix}
=
\begin{Bmatrix}
-P_e \\
-\frac{E_s \alpha_s T}{1-\nu_s}\cdot\frac{r_4{}^2-r_3{}^2}{2\cdot
r_4{}^2} \\
\frac{1+\nu_s}{1-\nu_s}\alpha_s T \cdot\frac{r_4{}^2-r_3{}^2}{2\cdot
r_4} \\
-\frac{E_c \alpha_c T}{1-\nu_c}\cdot\frac{r_3{}^2-r_2{}^2}{2\cdot
r_3{}^2} \\
\frac{1+\nu_c}{1-\nu_c}\alpha_c T \cdot\frac{r_3{}^2-r_2{}^2}{2\cdot
r_3} \\
-\frac{E_s \alpha_s T}{1-\nu_s}\cdot\frac{r_2{}^2-r_1{}^2}{2\cdot
r_2{}^2} \\
\frac{1+\nu_s}{1-\nu_s}\alpha_s T \cdot\frac{r_2{}^2-r_1{}^2}{2\cdot
r_2} \\
-\frac{E_c \alpha_c T}{1-\nu_c}\cdot\frac{r_1{}^2-r_a{}^2}{2\cdot
r_1{}^2} \\
\frac{1+\nu_c}{1-\nu_c}\alpha_c T \cdot\frac{r_1{}^2-r_a{}^2}{2\cdot
r_1} \\
0 \\
\end{Bmatrix}
\end{equation}
\begin{align*}
&a_{1,1}=\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)} &~&a_{1,2}=-\cfrac{E_c}{1+\nu_c}\cdot\cfrac{1}{r_b{}^2} &~& &~& \\
&a_{2,1}=\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)} & &a_{2,2}=-\cfrac{E_c}{1+\nu_c}\cdot\cfrac{1}{r_4{}^2} & &a_{2,3}=-\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{2,4} =\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_4{}^2} \\
&a_{3,1}=r_4 & &a_{3,2}=\frac{1}{r_4} & &a_{3,3}=-r_4 & &a_{3,4} =-\cfrac{1}{r_4} \\
&a_{4,3}=\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{4,4}=-\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_3{}^2} & &a_{4,5}=-\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)} & &a_{4,6} =\cfrac{E_c}{1+\nu_c}\cdot\cfrac{1}{r_3{}^2} \\
&a_{5,3}=r_3 & &a_{5,4}=\frac{1}{r_3} & &a_{5,5}=-r_3 & &a_{5,6} =-\cfrac{1}{r_3} \\
&a_{6,5}=\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)} & &a_{6,6}=-\cfrac{E_c}{1+\nu_c}\cdot\cfrac{1}{r_2{}^2} & &a_{6,7}=-\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{6,8} =\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_2{}^2} \\
&a_{7,5}=r_2 & &a_{7,6}=\frac{1}{r_2} & &a_{7,7}=-r_2 & &a_{7,8} =-\cfrac{1}{r_2} \\
&a_{8,7}=\cfrac{E_s}{(1+\nu_s)(1-2\nu_s)} & &a_{8,8}=-\cfrac{E_s}{1+\nu_s}\cdot\cfrac{1}{r_1{}^2} & &a_{8,9}=-\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)} & &a_{8,10}=\cfrac{E_c}{1+\nu_c}\cdot\cfrac{1}{r_1{}^2} \\
&a_{9,7}=r_1 & &a_{9,8}=\frac{1}{r_1} & &a_{9,9}=-r_1 & &a_{9,10}=-\cfrac{1}{r_1} \\
&a_{10,9}=\cfrac{E_c}{(1+\nu_c)(1-2\nu_c)} &~&a_{10,10}=-\cfrac{E_c}{1+\nu_c}\cdot\cfrac{1}{r_a{}^2} &~& &~& \\
\end{align*}
Example of the analysis
Comparison with the theoritical solution and the numerical solution
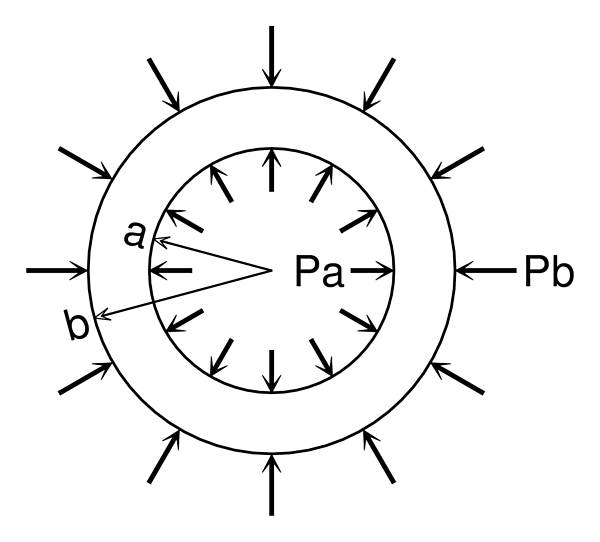
The comparison with the theoritical solution and the numerical solution were carried out using the model shown in below figure which was submitted to the internal water pressure or external water pressure.
The state of stress was the plane strain, and the characteristics of the material were that $E=25,000N/mm^2$ , $\nu=0.2$ , where $E$ is the elastick modulus and $\nu$ is Poisson's ratio.
\begin{equation*}
\begin{cases}
u=\cfrac{a^2}{b^2-a^2}\left(\cfrac{(1+\nu)(1-2\nu)}{E}\cdot
r+\cfrac{1+\nu}{E}\cdot\cfrac{b^2}{r}\right)\cdot P_a \\
~~~~-\cfrac{b^2}{b^2-a^2}\left(\cfrac{(1+\nu)(1-2\nu)}{E}\cdot
r+\cfrac{1+\nu}{E}\cdot\cfrac{a^2}{r}\right)\cdot P_b \\
\sigma_r=\cfrac{a^2}{b^2-a^2}\left(1-\cfrac{b^2}{r^2}\right)\cdot
P_a-\cfrac{b^2}{b^2-a^2}\left(1-\cfrac{a^2}{r^2}\right)\cdot P_b \\
\sigma_{\theta}=\cfrac{a^2}{b^2-a^2}\left(1+\cfrac{b^2}{r^2}\right)\cdot
P_a-\cfrac{b^2}{b^2-a^2}\left(1+\cfrac{a^2}{r^2}\right)\cdot P_b
\end{cases}
\end{equation*}
In above,
$\sigma_r$ means the stress in the radial direction, $\sigma_{\theta}$ means the stress in the circumferential direction, $u$ means the displacement in the radial direction.
| Theoritical solution (1) |
|---|
| $a$ | $b$ | $P_a$ | $P_b$ | $\sigma_{r(a)}$ | $\sigma_{\theta(a)}$ | $\sigma_{r(b)}$ | $\sigma_{\theta(b)}$ | $u_a$ | $u_b$ |
| 3000 | 3600 | 1 | 0 | -1.000 | 5.545 | 0.000 | 4.545 | 0.668 | 0.628 |
| 4000 | 4800 | 1 | 0 | -1.000 | 5.545 | 0.000 | 4.545 | 0.890 | 0.838 |
| 5000 | 6000 | 1 | 0 | -1.000 | 5.545 | 0.000 | 4.545 | 1.113 | 1.047 |
| 3000 | 3600 | 0 | 1 | 0.000 | -6.545 | -1.000 | -5.545 | -0.754 | -0.732 |
| 4000 | 4800 | 0 | 1 | 0.000 | -6.545 | -1.000 | -5.545 | -1.005 | -0.976 |
| 5000 | 6000 | 0 | 1 | 0.000 | -6.545 | -1.000 | -5.545 | -1.257 | -1.220 |
| Numerical solution (2) |
|---|
| $a$ | $b$ | $P_a$ | $P_b$ | $\sigma_{r(a)}$ | $\sigma_{\theta(a)}$ | $\sigma_{r(b)}$ | $\sigma_{\theta(b)}$ | $u_a$ | $u_b$ |
| 3000 | 3600 | 1 | 0 | -1.000 | 5.562 | 0.000 | 4.562 | 0.670 | 0.630 |
| 4000 | 4800 | 1 | 0 | -1.000 | 5.558 | 0.000 | 4.558 | 0.892 | 0.840 |
| 5000 | 6000 | 1 | 0 | -1.000 | 5.555 | 0.000 | 4.555 | 1.115 | 1.049 |
| 3000 | 3600 | 0 | 1 | 0.000 | -6.545 | -1.000 | -5.545 | -0.754 | -0.732 |
| 4000 | 4800 | 0 | 1 | 0.000 | -6.545 | -1.000 | -5.545 | -1.005 | -0.976 |
| 5000 | 6000 | 0 | 1 | 0.000 | -6.545 | -1.000 | -5.545 | -1.257 | -1.220 |
| Ratio (2)/(1) |
|---|
| $a$ | $b$ | $P_a$ | $P_b$ | $\sigma_{r(a)}$ | $\sigma_{\theta(a)}$ | $\sigma_{r(b)}$ | $\sigma_{\theta(b)}$ | $u_a$ | $u_b$ |
|
|
|
| 1.000 | 1.003 | --- | 1.004 | 1.004 | 1.003 |
|
|
|
| 1.000 | 1.002 | --- | 1.003 | 1.002 | 1.003 |
|
|
|
| 1.000 | 1.002 | --- | 1.002 | 1.002 | 1.002 |
|
|
|
| --- | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
|
|
|
| --- | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
In case of the internal water pressure submitted
The concrete is no-tension material in the numerical solution. For this case, the concrete covers were set by 1mm and the re-bars were set as a thick material with the characteristics of the concrete.
Therefore, the effective thickness of the cylinder is smaller than that of theoritical solution by 2mm.
However, the differences of the displacement and stresses are within 0.5%.
In case of the external water pressure submitted
In this case, the characteristics of re-bars were replaced by those of the concrete.
The numerical solution accords in the theoritical solution with the precision of a decimal three columns.
Comparison with FEM
Model for analysis
The comparison with FEM and numerical solution by multiple cylinder theory shown in this page were carried out under the condition shown in below table.
| Item | Characteristics of the section |
|---|
| Type of cross section | Double re-bar | Single re-bar |
| Internal radius of the tunnel | 4,000 mm | 4,000 mm |
| Thickness of the concrete | 800 mm | 600 mm |
| Outer radius of the bedrock area | 50,000 mm | 50,000 mm |
| Concrete cover | 100 mm | 100 mm |
| Inner re-bar | D32@200x2 | D25@250 |
| (equivalent steel plate thickness) | 3.97 mm | 2.03 mm |
| Outer re-bar | D32@200x2 | --- |
| (equivalent steel plate thickness) | 3.97 mm | --- |
| Elastic modulus of the concrete | 25,000 N/mm$^2$ |
| Poisson7s ratio of the concrete | 0.2 (zero for No-tension material) |
| Coefficient of Thermal expansion of the concrete | 10$\times$10$^{-6}$ $^\circ$C$^{-1}$ |
| Elastic modulus of the re-bar | 200,000 N/mm$^2$ |
| Poisson's ratio of the re-bar | 0.3 |
| Coefficient of thermal expansion of the re-bar | 10$\times$10$^{-6}$ $^\circ$C$^{-1}$ |
| Elastic modulus of the bedrock | 1$\sim$100,000 N/mm$^2$ |
| Poisson's ratio of the bedrock | 0.25 |
| Coefficient of thermal expansion of the bedrock | (no temperature change) |
| Internal water presure | 1 MPa |
| Temperature change of the RC structure | $-$10 $^\circ$C (uniform distribution) |
Results
| Result by the Multiple Cylinder Theory (1) |
|---|
| | Double reinforcement section | Single reinforcement section |
|---|
| $E_g$ | $\sigma_{sa}$ | $\sigma_{sb}$ | $\sigma_{rg}$ | $\sigma_{\theta g}$ | $u_a$ | $u_b$ | $\sigma_{sa}$ | $\sigma_{rg}$ | $\sigma_{\theta g}$ | $u_a$ | $u_b$ |
| 1 | 536.675 | 468.947 | -0.002 | 0.002 | 9.505 | 9.344 | 1955.928 | -0.006 | 0.006 | 35.986 | 35.914 |
| 10 | 527.569 | 460.987 | -0.016 | 0.015 | 9.335 | 9.174 | 1834.451 | -0.060 | 0.058 | 33.719 | 33.646 |
| 100 | 451.932 | 394.871 | -0.133 | 0.128 | 7.924 | 7.761 | 1136.818 | -0.368 | 0.356 | 20.701 | 20.625 |
| 1000 | 200.003 | 174.651 | -0.523 | 0.505 | 3.222 | 3.056 | 258.703 | -0.755 | 0.730 | 4.316 | 4.235 |
| 10000 | 59.570 | 51.894 | -0.741 | 0.714 | 0.601 | 0.433 | 57.164 | -0.844 | 0.816 | 0.555 | 0.473 |
| 100000 | 38.825 | 33.759 | -0.773 | 0.745 | 0.213 | 0.045 | 34.369 | -0.854 | 0.826 | 0.130 | 0.048 |
| Result by FEM (2) |
|---|
| | Double reinforcement section | Single reinforcement section |
|---|
| $E_g$ | $\sigma_{sa}$ | $\sigma_{sb}$ | $\sigma_{rg}$ | $\sigma_{\theta g}$ | $u_a$ | $u_b$ | $\sigma_{sa}$ | $\sigma_{rg}$ | $\sigma_{\theta g}$ | $u_a$ | $u_b$ |
| 1 | 536.491 | 468.795 | -0.002 | 0.002 | 9.499 | 9.398 | 1958.900 | -0.006 | 0.006 | 36.032 | 35.961 |
| 10 | 527.304 | 460.764 | -0.015 | 0.015 | 9.328 | 9.226 | 1836.720 | -0.058 | 0.056 | 33.753 | 33.681 |
| 100 | 451.034 | 394.092 | -0.129 | 0.128 | 7.905 | 7.802 | 1136.380 | -0.353 | 0.345 | 20.688 | 20.612 |
| 1000 | 197.480 | 172.449 | -0.504 | 0.532 | 3.174 | 3.067 | 258.149 | -0.722 | 0.743 | 4.305 | 4.224 |
| 10000 | 56.466 | 49.182 | -0.697 | 1.148 | 0.542 | 0.434 | 57.101 | -0.789 | 1.240 | 0.554 | 0.472 |
| 100000 | 35.654 | 30.989 | -0.556 | 5.329 | 0.154 | 0.045 | 34.373 | -0.619 | 5.397 | 0.130 | 0.048 |
| Ratio (2)/(1) |
|---|
| | Double reinforcement section | Single reinforcement section |
|---|
| $E_g$ | $\sigma_{sa}$ | $\sigma_{sb}$ | $\sigma_{rg}$ | $\sigma_{\theta g}$ | $u_a$ | $u_b$ | $\sigma_{sa}$ | $\sigma_{rg}$ | $\sigma_{\theta g}$ | $u_a$ | $u_b$ |
| 1 | 1.000 | 1.000 | 0.775 | 0.767 | 0.999 | 1.006 | 1.002 | 1.027 | 0.997 | 1.001 | 1.001 |
| 10 | 0.999 | 1.000 | 0.950 | 1.005 | 0.999 | 1.006 | 1.001 | 0.962 | 0.967 | 1.001 | 1.001 |
| 100 | 0.998 | 0.998 | 0.967 | 1.001 | 0.998 | 1.005 | 1.000 | 0.960 | 0.969 | 0.999 | 0.999 |
| 1000 | 0.987 | 0.987 | 0.964 | 1.053 | 0.985 | 1.004 | 0.998 | 0.957 | 1.018 | 0.997 | 0.997 |
| 10000 | 0.948 | 0.948 | 0.941 | 1.608 | 0.902 | 1.002 | 0.999 | 0.935 | 1.520 | 0.998 | 0.998 |
| 100000 | 0.918 | 0.918 | 0.719 | 7.153 | 0.723 | 1.009 | 1.000 | 0.725 | 6.534 | 1.000 | 0.996 |
Comments
- The stresses of re-bar decrease inthe result of FEM with an increase in the elastic modulus of the bedrock.
However, this is not significant problem because the absolute value of stress is very small.
- In the case of large elastic modulus of the bedrock, the difference of stress value of the bedrock betwen FEM result and MCT result becomes large.
This is caused by the treatment of the temperature change.
In MCT (multiple cylinder theory), only the displacement of the concrete affect to the stress of the bedock.
Whereas, in FEM, the temperature change affect to the bedrock element directly, because the temperature changes are inputted on the nodes of boundary between the concrete and the bedrock.
- The solution by the mutiple cylinder theory is equivalent to the strict solution theoretically, and the stresses of re-bar by FEM are smaller than that by MCT.
However, if we want to evaluate the effect of the temperature change with accuracy, it is convenient to use the FEM.
Because the strict treatment of the temperature change is too complicated in the treatment of the equations.
Programs
Program and sample data
Script for execution
gfortran -o f90_rcpt f90_rcpt.f90
./f90_rcpt inp_cpt_test.csv out_cpt_test.csv
./f90_rcpt inp_cpt_comp.csv out_cpt_comp.csv
Source code and sample data
Input data
Cooemnt for output
# line for comment
IE, PP, TT, aa, bb, rr, cc, ta, tb, Ec, nc, ac, Es, ns, as, Eg, ng
・・・・・
- Comment for output is written in the first line
- # means a line for comment
- Data for calculation shall be written in 1 line for 1 case of calculation with CSV.
- The sequence of data is shown below:
| IE | 0: for internal pressure, 1: for external pressure |
| PP | Water pressure (for internal pressure: outer direction is positive, for extenal pressure: inner direction is positive) |
| TT | Temperature change (positive: tenperature increase) |
| aa | Internal radius of the circular tunnel |
| bb | Excavated radius (outer radius of the concrete) |
| rr | Outer radius of the bedrock |
| cc | Concrete cover (outer cover has the same value as the inner cover) |
| ta | Equivalent steel plate thickness of inner re-bar |
| tb | Equivalent steel plate thickness of outer re-bar |
| Ec | Elastic modulus of the concrete |
| nc | Poisson's ratio of the concrete |
| ac | Coefficient of thermal expansion of the concrete |
| Es | Elastic modulus of the re-bar |
| ns | Poisson's ratio of the re-bar |
| as | Coefficient of thermal expansion of the re-bar |
| Eg | Elastic modulus of the bedrock |
| ng | Poisson's ratio of the bedrock |
Output data
Comment for output
*Input data
k, IE, PP, TT, aa, bb, rr, cc, ta, tb, Ec, nc, ac, Es, ns, as, Eg, ng
..... comma selected value .....
..... ..... .....
*Output data
k, IE, Eg, dT, sr_c, st_c, sr_si1, st_si1, sr_si2, st_si2, sr_so1, st_so1, sr_so2, st_so2, sr_g, st_g, ua, ub
..... comma selected value .....
..... ..... .....
| k | No. of the case | | IE | 0: for the internal pressure, 1: for the external pressure |
| Eg | Elastic modulus of the bedrock | | dT | Temperature change |
| sr_c | Stress of concrete in the radial direction | | st_c | Stress of the concrete in the circumferential direction |
| sr_si1 | Stress of inner re-bar in the radial direction at inner side | | st_si1 | Stress of inner re-bar in the circumferential direction at inner side |
| sr_si2 | Stress of inner re-bar in the radial direction at outer side | | st_si2 | Stress of inner re-bar in the circumferential direction at outer side |
| sr_so1 | Stress of outer re-bar in the radial direction at inner side | | st_so1 | Stress of outer re-bar in the circumferential direction at inner side |
| sr_so2 | Stress of outer re-bar in the radial direction at outer side | | st_so2 | Stress of outer re-bar in the circumferential direction at outer side |
| sr_g | Stress of the bedrock in the radial direction at the inner boundary | | st_g | Stress of the bedrock in the circumferential direction at the inner boundary |
| ua | Displacement at the inner surface of the concrete (positive: outer direction) | | ub | Displacement at the outer surface of the concrete (positive: outer direction) |





