積分の考え方
直行座標系 $x-y$ 平面上のある領域で定義されている関数 $f(x,y)$ を，定義領域内の指定された形状の面積上で積分することを考える． ここでいう「指定された形状」とは，長方形領域とは限らない．この指定された形状の面積上での積分の考え方は以下のとおりとする．
- 指定したい領域を多角形で近似する
- 多角形近似された領域を更に有限個(例えば $n$ 個)の四角形の集合体に置き換える
- 個々の四角形領域で関数の積分値を求め，これらの総和をとることにより指定した領域の積分値とみなす
- 個々の四角形領域の形状も都合よく長方形であるとは限らないため，任意形状の四角形領域の積分を， $-1 \leqq a \leqq 1$ および $-1 \leqq b \leqq 1$ で定義される正方形領域の積分に置き換え処理する． このためには積分の変数変換を行う必要があることに注意．
- 以上を式に表すと，以下のとおり表現できる
\begin{equation}
\int\int_{S} f(x,y) ds \doteqdot \sum_{i=1}^{n} \int\int_{s_i} f(x,y) ds_i = \sum_{i=1}^{n} \left\{\int_{-1}^{1}\int_{-1}^{1} f(x(a),y(b)) \cdot \det[J(a,b)] da db\right\}_{i}
\end{equation}
変数変換(座標変換)
任意形状の四角形領域の積分を， $-1 \leqq a \leqq 1$ および $-1 \leqq b \leqq 1$ で定義される正方形領域の積分に置き換えるための変数変換(座標変換)の方法を考える． この処理は，積分の方法としては変数変換であるが，幾何学的意味は座標変換となる．
任意形状四角形領域の定義
積分したい領域を分割して得られた小さな四角形領域を考え，これを要素と称することにする． この要素(四角形領域)は，以下の性質を持つものとする．
- 要素の頂点はそれぞれ異なる4つの座標 $(x,y)$ を持つ．これを節点と称することとする．
- 隣り合う辺で構成される角度は180度未満とする．すなわち凹型部を含まない．
- 節点(四角形の頂点)に名前をつける．それぞれ $i$，$j$，$k$，$l$ とする．順番は $(x,y)$ 座標値の大小には関係なく，必ず反時計回りでなければならない．
要素内任意位置座標を節点座標で表す
まず，要素内任意位置を節点座標を用いて表現することを考える．要素内任意位置の座標 $(x,y)$ が以下で表されるとする．
\begin{align}
& x=N_1(a,b)x_i+N_2(a,b)x_j+N_3(a.b)x_k+N_4(a,b)x_l \\
& y=N_1(a,b)y_i+N_2(a,b)y_j+N_3(a.b)y_k+N_4(a,b)y_l \\
\end{align}
ここに $[N]$ は $-1 \leqq a \leqq 1$ および $-1 \leqq b \leqq 1$ で定義される変数 $(a,b)$ の関数であり，以下のものを用いることができる．
\begin{equation}
N_1=\cfrac{1}{4}(1-a)(1-b) \qquad
N_2=\cfrac{1}{4}(1+a)(1-b) \qquad
N_3=\cfrac{1}{4}(1+a)(1+b) \qquad
N_4=\cfrac{1}{4}(1-a)(1+b)
\end{equation}
以下，jacobian計算に必要な諸量を示す．
\begin{align}
& \cfrac{\partial N_1}{\partial a}=-\cfrac{1}{4}(1-b)
& \cfrac{\partial N_2}{\partial a}=+\cfrac{1}{4}(1-b)
& \cfrac{\partial N_3}{\partial a}=+\cfrac{1}{4}(1+b)
& \cfrac{\partial N_4}{\partial a}=-\cfrac{1}{4}(1+b) \\
& \cfrac{\partial N_1}{\partial b}=-\cfrac{1}{4}(1-a)
& \cfrac{\partial N_2}{\partial b}=-\cfrac{1}{4}(1+a)
& \cfrac{\partial N_3}{\partial b}=+\cfrac{1}{4}(1+a)
& \cfrac{\partial N_4}{\partial b}=+\cfrac{1}{4}(1-a)
\end{align}
\begin{equation}
[J]=
\begin{bmatrix}
\cfrac{\partial x}{\partial a} & \cfrac{\partial y}{\partial a} \\
\cfrac{\partial x}{\partial b} & \cfrac{\partial y}{\partial b}
\end{bmatrix}
=
\begin{bmatrix}
J_{11} & J_{12} \\
J_{21} & J_{22}
\end{bmatrix}
\end{equation}
\begin{align}
&J_{11}(a,b)=\cfrac{\partial N_1}{\partial a} x_i + \cfrac{\partial N_2}{\partial a} x_j + \cfrac{\partial N_3}{\partial a} x_k + \cfrac{\partial N_4}{\partial a} x_l \\
&J_{12}(a,b)=\cfrac{\partial N_1}{\partial a} y_i + \cfrac{\partial N_2}{\partial a} y_j + \cfrac{\partial N_3}{\partial a} y_k + \cfrac{\partial N_4}{\partial a} y_l \\
&J_{21}(a,b)=\cfrac{\partial N_1}{\partial b} x_i + \cfrac{\partial N_2}{\partial b} x_j + \cfrac{\partial N_3}{\partial b} x_k + \cfrac{\partial N_4}{\partial b} x_l \\
&J_{22}(a,b)=\cfrac{\partial N_1}{\partial b} y_i + \cfrac{\partial N_2}{\partial b} x_y + \cfrac{\partial N_3}{\partial b} y_k + \cfrac{\partial N_4}{\partial b} y_l
\end{align}
\begin{equation}
\det[J(a,b)]=J_{11}(a,b) \cdot J_{22}(a,b) - J_{12}(a,b) \cdot J_{21}(a,b)
\end{equation}
以上により，Jacobian (Jacobi行列の行列式) の値 $\det[J]$ が計算できるわけであるが，この値は定数ではなく， $(a,b)$ の関数であることを忘れないように！
Simpson法
各四角形要素毎の積分値 $S$ は以下の計算により求めることができる．
\begin{align}
&s_{11}= f(x(a_1,b_1),y(a_1,b_1)) \cdot \det[J(a_1,b_1)] \\
&s_{12}= f(x(a_1,b_2),y(a_1,b_2)) \cdot \det[J(a_1,b_2)] \\
&s_{13}= f(x(a_1,b_3),y(a_1,b_3)) \cdot \det[J(a_1,b_3)] \\
& \\
&s_{21}= f(x(a_2,b_1),y(a_2,b_1)) \cdot \det[J(a_2,b_1)] \\
&s_{22}= f(x(a_2,b_2),y(a_2,b_2)) \cdot \det[J(a_2,b_2)] \\
&s_{23}= f(x(a_2,b_3),y(a_2,b_3)) \cdot \det[J(a_2,b_3)] \\
& \\
&s_{31}= f(x(a_3,b_1),y(a_3,b_1)) \cdot \det[J(a_3,b_1)] \\
&s_{32}= f(x(a_3,b_2),y(a_3,b_2)) \cdot \det[J(a_3,b_2)] \\
&s_{33}= f(x(a_3,b_3),y(a_3,b_3)) \cdot \det[J(a_3,b_3)] \\
& \\
&S_1=\cfrac{1}{3}(s_{11}+4 s_{12}+s_{13}) \\
&S_2=\cfrac{1}{3}(s_{21}+4 s_{22}+s_{23}) \\
&S_3=\cfrac{1}{3}(s_{31}+4 s_{32}+s_{33}) \\
&S =\cfrac{1}{3}(S_1 + 4 S_2 + S_3)
\end{align}
関数値を計算したらその都度同じ座標で計算したJacobian( $\det[J(a,b)]$ )を乗じること，Simpson法適用時の第1項は積分区間が $-1 \sim 1$ になるため 1/6 ではなく 1/3 になることに注意する．
実際に用いられている積分点座標は，以下のとおり．
| i | j | ai | bj |
|---|---|---|---|
| 1 | 1 | -1.000 | -1.000 |
| 1 | 2 | -1.000 | 0.000 |
| 1 | 3 | -1.000 | 1.000 |
| 2 | 1 | 0.000 | -1.000 |
| 2 | 2 | 0.000 | 0.000 |
| 2 | 3 | 0.000 | 1.000 |
| 3 | 1 | 1.000 | -1.000 |
| 3 | 2 | 1.000 | 0.000 |
| 3 | 3 | 1.000 | 1.000 |
Gauss-Legendre積分
\begin{equation}
\int\int f(x,y) dx dy \doteqdot \sum_{i=1}^n \sum_{j=1}^n \left\{w_i \cdot w_j \cdot f\left(x(a_i,b_j),y(a_i,b_j)\right) \cdot \det[J(a_i,b_j)]\right\}
\end{equation}
$S=\sum_{i=1}^n \sum_{j=1}^n \left\{w_i w_j f(x(a_i,b_j),y(a_i,b_j))\det[J(a_i,b_j)]\right\}$ と置き，Simpson法との整合を考え，9積分点モデルとすれば，以下のように $S$ を求めることができる．
\begin{align}
&s_{11}=w_1 \cdot f(x(a_1,b_1),y(a_1,b_1)) \cdot \det[J(a_1,b_1)] \\
&s_{12}=w_2 \cdot f(x(a_1,b_2),y(a_1,b_2)) \cdot \det[J(a_1,b_2)] \\
&s_{13}=w_3 \cdot f(x(a_1,b_3),y(a_1,b_3)) \cdot \det[J(a_1,b_3)] \\
& \\
&s_{21}=w_1 \cdot f(x(a_2,b_1),y(a_2,b_1)) \cdot \det[J(a_2,b_1)] \\
&s_{22}=w_2 \cdot f(x(a_2,b_2),y(a_2,b_2)) \cdot \det[J(a_2,b_2)] \\
&s_{23}=w_3 \cdot f(x(a_2,b_3),y(a_2,b_3)) \cdot \det[J(a_2,b_3)] \\
& \\
&s_{31}=w_1 \cdot f(x(a_3,b_1),y(a_3,b_1)) \cdot \det[J(a_3,b_1)] \\
&s_{32}=w_2 \cdot f(x(a_3,b_2),y(a_3,b_2)) \cdot \det[J(a_3,b_2)] \\
&s_{33}=w_3 \cdot f(x(a_3,b_3),y(a_3,b_3)) \cdot \det[J(a_3,b_3)] \\
& \\
&S_1=s_{11}+s_{12}+s_{13} \\
&S_2=s_{21}+s_{22}+s_{23} \\
&S_3=s_{31}+s_{32}+s_{33} \\
& \\
&S=w_1 S_1 + w_2 S_2 + w_3 S_3
\end{align}
関数値を計算したらその都度同じ座標で計算したJacobian( $\det[J(a,b)]$ )を乗じることに注意する．
実際に用いられている重みおよび積分点座標は，以下のとおり．
| i | j | wi | wj | ai | bj |
|---|---|---|---|---|---|
| 1 | 1 | 0.555555555555555 | 0.555555555555555 | -0.774596669241483 | -0.774596669241483 |
| 1 | 2 | 0.555555555555555 | 0.888888888888889 | -0.774596669241483 | 0.000000000000000 |
| 1 | 3 | 0.555555555555555 | 0.555555555555555 | -0.774596669241483 | 0.774596669241483 |
| 2 | 1 | 0.888888888888889 | 0.555555555555555 | 0.000000000000000 | -0.774596669241483 |
| 2 | 2 | 0.888888888888889 | 0.888888888888889 | 0.000000000000000 | 0.000000000000000 |
| 2 | 3 | 0.888888888888889 | 0.555555555555555 | 0.000000000000000 | 0.774596669241483 |
| 3 | 1 | 0.555555555555555 | 0.555555555555555 | 0.774596669241483 | -0.774596669241483 |
| 3 | 2 | 0.555555555555555 | 0.888888888888889 | 0.774596669241483 | 0.000000000000000 |
| 3 | 3 | 0.555555555555555 | 0.555555555555555 | 0.774596669241483 | 0.774596669241483 |
Programs
Programs
| Filename | Description |
|---|---|
| a_f90.txt | Shell script for execution |
| f90_adint3.f90 | 2-dim Gauss-Legendre integration |
| f90_adsimp.f90 | 2-dim Simpson integration |
| ms_018.txt | Input data sample of approxmate circle domain with 18 sides |
| ms_036.txt | Input data sample of approxmate circle domain with 36 sides |
| ms_072.txt | Input data sample of approxmate circle domain with 72 sides |
| ms_090.txt | Input data sample of approxmate circle domain with 90 sides |
積分領域指定データファイルの書式
NODT NELT ! 総節点数 総要素数 kakom(1,1) kakom(1,2) kakom(1,3) kakom(1,4) ! 要素番号 1 を構成する4つの節点番号 kakom(2,1) kakom(2,2) kakom(2,3) kakom(2,4) ! 要素番号 2 を構成する4つの節点番号 kakom(3,1) kakom(3,2) kakom(3,3) kakom(3,4) ! 要素番号 3 を構成する4つの節点番号 .... .... .... ! kakom(NELT,1) kakom(NELT,2) kakom(NELT,3) kakom(NELT,4) ! 要素番号 NELT を構成する4つの節点番号 x(1) y(1) ! 節点 1 のx-y座標 x(2) y(2) ! 節点 2 のx-y座標 x(3) y(3) ! 節点 3 のx-y座標 .... .... ! x(NODT) y(NODT) ! 節点 NODT のx-y座標
計算結果事例(1)
半径1，中心(0,0)の円を辺数18，36，72，90の正多角形に近似し， $\pi$ の値を求めた， 積分関数は以下のとおり．積分領域 $S$ は，円形領域を多角形に近似した領域． この場合，被積分関数は定数値なので，結果は与えた領域の精度に依存し，Simpson法，Gauss法による差異は無い．
\begin{equation}
\iint_S 1 = \pi
\end{equation}
| Simpson | ||||
|---|---|---|---|---|
| Side | NODT | NELT | Area | Estimated |
| 18 | 97 | 78 | 3.078181401376 | 3.078181401376 |
| 36 | 377 | 340 | 3.125667311168 | 3.125667311168 |
| 72 | 1377 | 1304 | 3.137607074920 | 3.137607074920 |
| 90 | 1473 | 1382 | 3.139041953451 | 3.139041953451 |
| Gauss-Legendre | ||||
|---|---|---|---|---|
| Side | NODT | NELT | Area | Estimated |
| 18 | 97 | 78 | 3.078181401376 | 3.078181401376 |
| 36 | 377 | 340 | 3.125667311168 | 3.125667311168 |
| 72 | 1377 | 1304 | 3.137607074920 | 3.137607074920 |
| 90 | 1473 | 1382 | 3.139041953451 | 3.139041953451 |
上表中の記号の意味は以下のとおり．
| Side | ：近似した辺数 |
| NODE | ：積分領域の四角形を構成する節点数 |
| NELT | ：積分領域の四角形を構成する要素 |
| Area | ：積分領域の多角形総面積(真値) |
| Estimated | ：計算値 |
計算結果事例(2)
半径1，中心(0,0)の円を辺数18，36，72，90の正多角形に近似し， $\pi$ の値を求めた， 積分関数は以下のとおり．積分領域 $S$ は，円形領域を多角形に近似した領域． この場合，上半球の積分値を求めるため，結果は与えた領域の精度と手法の違いによる精度差が現れる．
\begin{equation}
\cfrac{3}{2} \iint_S \sqrt{1-x^2-y^2} = \pi
\end{equation}
| Simpson | ||||
|---|---|---|---|---|
| Side | NODT | NELT | Area | Estimated |
| 18 | 97 | 78 | 3.078181401376 | 3.117509819579 |
| 36 | 377 | 340 | 3.125667311168 | 3.134940218856 |
| 72 | 1377 | 1304 | 3.137607074920 | 3.139317101760 |
| 90 | 1473 | 1382 | 3.139041953451 | 3.139358623356 |
| Gauss-Legendre | ||||
|---|---|---|---|---|
| Side | NODT | NELT | Area | Estimated |
| 18 | 97 | 78 | 3.078181401376 | 3.133077864602 |
| 36 | 377 | 340 | 3.125667311168 | 3.140860323439 |
| 72 | 1377 | 1304 | 3.137607074920 | 3.141636977099 |
| 90 | 1473 | 1382 | 3.139041953451 | 3.141719782623 |
上表中の記号の意味は以下のとおり．
| Side | ：近似した辺数 |
| NODE | ：積分領域の四角形を構成する節点数 |
| NELT | ：積分領域の四角形を構成する要素 |
| Area | ：積分領域の多角形総面積(真値) |
| Estimated | ：計算値 |
積分領域の分割図
| 円周方向 18 分割 | 円周方向 36 分割 |
|---|---|
 |
 |
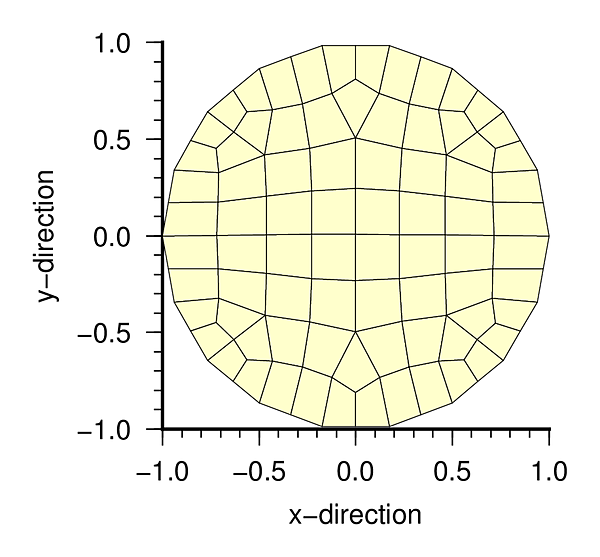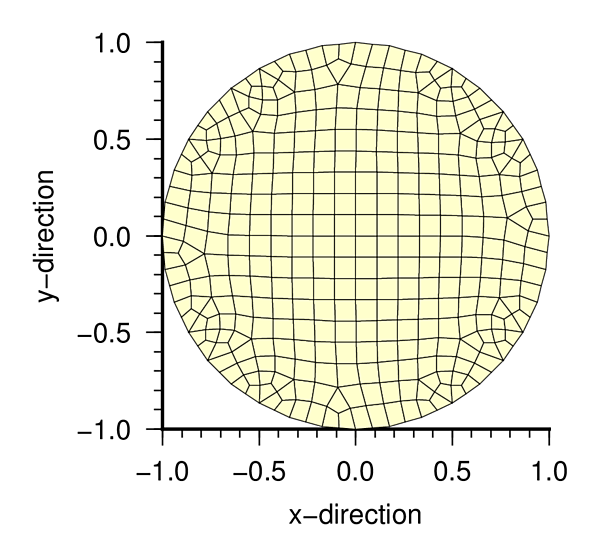| 円周方向 72 分割 | 円周方向 90 分割 |
 |
 |
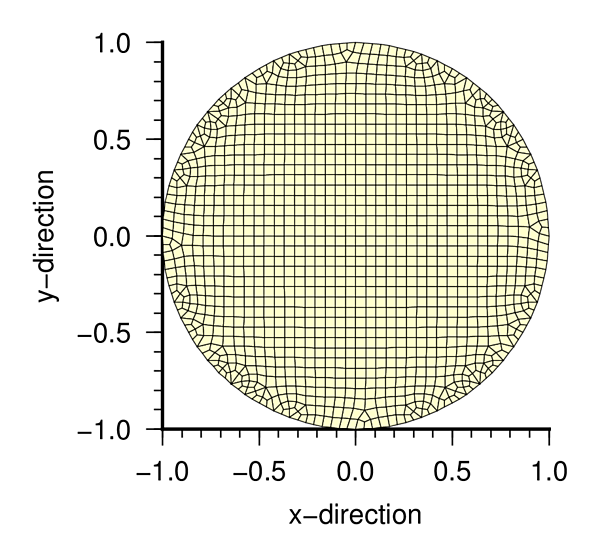
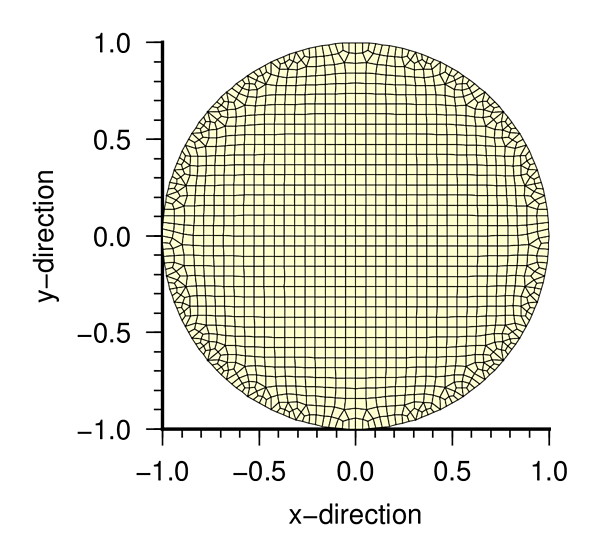