Simpson法
比較的小さい積分領域 $x_a \leqq x \leqq x_b$ を領域を考えたとき,一次元のSimpson法は以下のとおり表現できた.
\begin{equation}
\int_{x_a}^{x_b} f(x) dx = \cfrac{x_b-x_a}{6} \left\{f(x_a) + 4 f \left(\cfrac{x_a+x_b}{2}\right) + f(x_b)\right\}
\end{equation}
上式を二次元に拡張することを考える.積分領域は $x_a \leqq x \leqq x_b$,$y_a \leqq y \leqq y_b$ の長方形領域を考え, 表現の単純化のため,積分領域の中間点 $x_c=(x_a+x_b)/2$,$y_c=(y_a+y_b)/2$ を定義しておく.
まず $y$ 方向の3測線を考え,それぞれの積分値を $s_1$,$s_2$,$s_3$ とし,これを $x$ 方向で積分することを考えると,以下のように2重積分値 $S$ が定められる
\begin{align}
&s_1=\cfrac{y_b-y_a}{6}\left\{f(x_a,y_a)+4 f(x_a,y_c)+f(x_a,y_b)\right\}\\
&s_2=\cfrac{y_b-y_a}{6}\left\{f(x_c,y_a)+4 f(x_c,y_c)+f(x_c,y_b)\right\}\\
&s_3=\cfrac{y_b-y_a}{6}\left\{f(x_b,y_a)+4 f(x_b,y_c)+f(x_b,y_b)\right\}\\
&S=\cfrac{x_b-x_a}{6}(s_1 + 4 s_2 + s_3)
\end{align}
Gauss-Legendre積分
Gauss-Legendre積分の積分点および積分値は,積分領域が $-1 \leqq u \leqq 1$,$-1 \leqq v \leqq 1$ で与えられるため,任意の領域を積分するためには,変数変換を考える必要がある. 一般に,Jacobi行列を$[J]$として
\begin{equation}
\int\int f(x,y)dx dy=\int\int f\left(x(u,v),y(u,v)\right) \det[J] du dv
\end{equation}
ここで, $x_a \leqq x \leqq x_b$,$y_a \leqq y \leqq y_b$ の長方形領域を考えた場合,Gauss-legendre積分では
\begin{equation}
x(u,v)=\cfrac{x_b-x_a}{2}u+\cfrac{x_a+x_b}{2} \qquad\qquad y(u,v)=\cfrac{y_b-y_a}{2}v+\cfrac{y_a+y_b}{2}
\end{equation}
であるから,Jacobi行列 $[J]$ およびJacobian(jacobi行列の行列式) $\det[J]$ は,
\begin{equation}
[J]=
\begin{bmatrix}
\cfrac{\partial x}{\partial u} & \cfrac{\partial x}{\partial v} \\
\cfrac{\partial y}{\partial u} & \cfrac{\partial y}{\partial v}
\end{bmatrix}
=
\begin{bmatrix}
\cfrac{x_b-x_a}{2} & 0\\
0 & \cfrac{y_b-y_a}{2}
\end{bmatrix}
\qquad\qquad
\det[J]=\cfrac{(x_b-x_a)(y_b-y_a)}{4}
\end{equation}
となる. したがって,Gauss-Legendre積分の定義により
\begin{equation}
\int\int f(x,y) dx dy \doteqdot \sum_{i=1}^n \sum_{j=1}^n \left\{w_i w_j f\left(x(u_i),y(v_j)\right)\right\} \cdot \cfrac{(x_b-x_a)(y_b-y_a)}{4}
\end{equation}
$S'=\sum_{i=1}^n \sum_{j=1}^n \left\{w_i w_j f(x(u_i),y(v_j))\right\}$ と置き,Simpson法との整合を考え,9積分点モデルとすれば,以下のように $S'$ を求めることができる.
\begin{align}
S'=&w_1 \left\{w_1 f(x(u_1),y(v_1)) + w_2 f(x(u_1),y(v_2)) + w_3 f(x(u_1),y(v_3))\right\}\\
+&w_2 \left\{w_1 f(x(u_2),y(v_1)) + w_2 f(x(u_2),y(v_2)) + w_3 f(x(u_2),y(v_3))\right\}\\
+&w_3 \left\{w_1 f(x(u_3),y(v_1)) + w_2 f(x(u_3),y(v_2)) + w_3 f(x(u_3),y(v_3))\right\}
\end{align}
実際に用いられている重みおよび積分点座標は,以下のとおり.
| i | j | wi | wj | ai | bj |
|---|---|---|---|---|---|
| 1 | 1 | 0.555555555555555 | 0.555555555555555 | -0.774596669241483 | -0.774596669241483 |
| 1 | 2 | 0.555555555555555 | 0.888888888888889 | -0.774596669241483 | 0.000000000000000 |
| 1 | 3 | 0.555555555555555 | 0.555555555555555 | -0.774596669241483 | 0.774596669241483 |
| 2 | 1 | 0.888888888888889 | 0.555555555555555 | 0.000000000000000 | -0.774596669241483 |
| 2 | 2 | 0.888888888888889 | 0.888888888888889 | 0.000000000000000 | 0.000000000000000 |
| 2 | 3 | 0.888888888888889 | 0.555555555555555 | 0.000000000000000 | 0.774596669241483 |
| 3 | 1 | 0.555555555555555 | 0.555555555555555 | 0.774596669241483 | -0.774596669241483 |
| 3 | 2 | 0.555555555555555 | 0.888888888888889 | 0.774596669241483 | 0.000000000000000 |
| 3 | 3 | 0.555555555555555 | 0.555555555555555 | 0.774596669241483 | 0.774596669241483 |
Programs
Programs
| Filename | Description |
|---|---|
| a_f90.txt | Shell script for execution |
| a_gmt.txt | GMT command for drawing |
| f90_dgint3.f90 | 2-dim Gauss-Legendre integration |
| f90_dsimp.f90 | 2-dim Simpson integration |
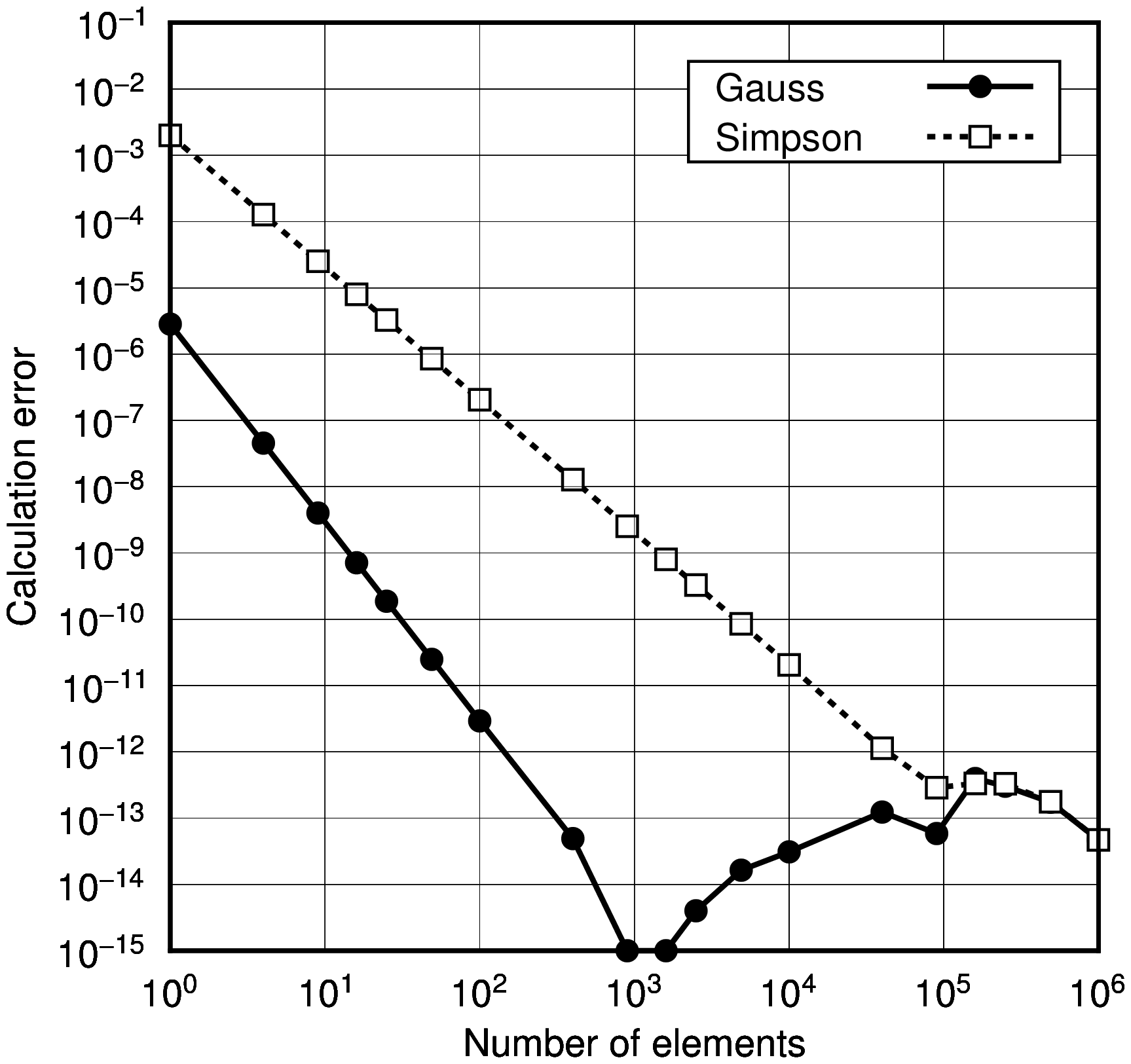
解の収束状況作図事例
以下に計算事例を示す.積分した式は以下のとおり.
\begin{equation}
\int_0^1 \int_0^1 \exp(x+y) dx dy = (e-1)^2
\end{equation}
| Simpson | |||
|---|---|---|---|
| nx | ny | Estimated value | Error |
| 1 | 1 | 0.295448365943E+01 | +0.199121741797E-02 |
| 2 | 2 | 0.295261964250E+01 | +0.127200490735E-03 |
| 3 | 3 | 0.295251767147E+01 | +0.252294546619E-04 |
| 4 | 4 | 0.295250043629E+01 | +0.799428018006E-05 |
| 5 | 5 | 0.295249571866E+01 | +0.327664674993E-05 |
| 7 | 7 | 0.295249329545E+01 | +0.853435002668E-06 |
| 10 | 10 | 0.295249264699E+01 | +0.204973195750E-06 |
| 20 | 20 | 0.295249245483E+01 | +0.128136812272E-07 |
| 30 | 30 | 0.295249244454E+01 | +0.253120102656E-08 |
| 40 | 40 | 0.295249244281E+01 | +0.800902455467E-09 |
| 50 | 50 | 0.295249244234E+01 | +0.328065574706E-09 |
| 70 | 70 | 0.295249244210E+01 | +0.853996873218E-10 |
| 100 | 100 | 0.295249244203E+01 | +0.204396499726E-10 |
| 200 | 200 | 0.295249244201E+01 | +0.113864473406E-11 |
| 300 | 300 | 0.295249244201E+01 | +0.287325718773E-12 |
| 400 | 400 | 0.295249244201E+01 | -0.339284156325E-12 |
| 500 | 500 | 0.295249244201E+01 | +0.329514193709E-12 |
| 700 | 700 | 0.295249244201E+01 | +0.198507876803E-12 |
| 1000 | 1000 | 0.295249244201E+01 | +0.244249065418E-13 |
| Gauss-Legendre | |||
|---|---|---|---|
| nx | ny | Estimated value | Error |
| 1 | 1 | 0.295248960999E+01 | -0.283202512019E-05 |
| 2 | 2 | 0.295249239663E+01 | -0.453798536526E-07 |
| 3 | 3 | 0.295249243801E+01 | -0.400277144763E-08 |
| 4 | 4 | 0.295249244130E+01 | -0.713587411383E-09 |
| 5 | 5 | 0.295249244183E+01 | -0.187207582769E-09 |
| 7 | 7 | 0.295249244199E+01 | -0.248818743387E-10 |
| 10 | 10 | 0.295249244201E+01 | -0.293143287422E-11 |
| 20 | 20 | 0.295249244201E+01 | -0.492939022934E-13 |
| 30 | 30 | 0.295249244201E+01 | +0.444089209850E-15 |
| 40 | 40 | 0.295249244201E+01 | +0.000000000000E+00 |
| 50 | 50 | 0.295249244201E+01 | +0.399680288865E-14 |
| 70 | 70 | 0.295249244201E+01 | -0.164313007645E-13 |
| 100 | 100 | 0.295249244201E+01 | -0.310862446895E-13 |
| 200 | 200 | 0.295249244201E+01 | -0.123456800338E-12 |
| 300 | 300 | 0.295249244201E+01 | +0.568434188608E-13 |
| 400 | 400 | 0.295249244201E+01 | -0.398792110445E-12 |
| 500 | 500 | 0.295249244201E+01 | +0.300648395068E-12 |
| 700 | 700 | 0.295249244201E+01 | +0.193178806285E-12 |
| 1000 | 1000 | 0.295249244201E+01 | +0.244249065418E-13 |
 |
