1質点系の運動方程式
時刻 $t+\Delta t$ での質点系の釣り合いを示す運動方程式は以下の通り．ここにドットは時間微分を示す．
\begin{equation}
m\cdot\ddot{u}(t+\Delta t)+c\cdot\dot{u}(t+\Delta t)+k\cdot u(t+\Delta t)=f(t+\Delta t)
\end{equation}
| ここに， | $m$ | ：質量 | $\ddot{u}$ | ：加速度 | $f$ | ：外力 | ||
| $c$ | ：減衰係数 | $\dot{u}$ | ：速度 | |||||
| $k$ | ：バネ定数 | $u$ | ：変位 |
運動方程式の解法：線形加速度法
変位
時刻 $t+\Delta t$ での変位 $u$ を Taylor 展開し， $\Delta t$ の 3 次項まで考慮することにより，以下の式が得られる．
\begin{align}
u(t+\Delta t)&=u(t)+\frac{\Delta t}{1!}\cdot\dot{u}(t)+\frac{(\Delta t)^2}{2!}\cdot\ddot{u}(t)+\frac{(\Delta t)^3}{3!}\cdot\dddot{u}(t)+\cdots \\
&=u(t)+\Delta t\cdot\dot{u}(t)+\frac{(\Delta t)^2}{3}\cdot\ddot{u}(t)+\frac{(\Delta t)^2}{6}\cdot\ddot{u}(t+\Delta t)
\end{align}
基本的な考え方として，全ての項を，時刻 $t$ と時刻 $t+\Delta t$ での加速度 $\ddot{u}$ ，速度 $\dot{u}$ ，変位 $u$ で表現したい． このため，線形加速度法では， $\Delta t$ の 3 次項を以下のように線形化して上式を得ている．
\begin{equation}
\dddot{u}(t)=\frac{\ddot{u}(t+\Delta t)-\ddot{u}(t)}{\Delta t}
\end{equation}
速度
加速度の積分を台形公式で近似することにより，以下の式が得られる．
\begin{equation}
\dot{u}(t+\Delta t)=\dot{u}(t)+\int_t^{t+\Delta t}\ddot{u}(t)dt
=\dot{u}(t)+\frac{\Delta t}{2}\cdot\left(\ddot{u}(t+\Delta t)+\ddot{u}(t)\right)
\end{equation}
加速度
これまでにもとめた変位・速度を運動方程式に代入することにより加速度が以下の通り求まる．
\begin{equation}
\ddot{u}(t+\Delta t)=
\cfrac{f(t+\Delta t)-c\cdot\left(\dot{u}(t)+\cfrac{\Delta t}{2}\cdot\ddot{u}(t)\right)-k\cdot\left(u(t)+\Delta t\cdot\dot{u}(t)+\cfrac{(\Delta t)^2}{3}\cdot\ddot{u}(t)\right)}
{m+c\cdot\cfrac{\Delta t}{2}+k\cdot\cfrac{(\Delta t)^2}{6}}
\end{equation}
線形加速度法まとめ
\begin{align}
\ddot{u}(t+\Delta t)=&
\cfrac{f(t+\Delta t)-c\cdot\left(\dot{u}(t)+\cfrac{\Delta t}{2}\cdot\ddot{u}(t)\right)-k\cdot\left(u(t)+\Delta t\cdot\dot{u}(t)+\cfrac{(\Delta t)^2}{3}\cdot\ddot{u}(t)\right)}
{m+c\cdot\cfrac{\Delta t}{2}+k\cdot\cfrac{(\Delta t)^2}{6}}\\
\dot{u}(t+\Delta t)=&
\dot{u}(t)+\frac{\Delta t}{2}\cdot\ddot{u}(t)+\frac{\Delta t}{2}\cdot\ddot{u}(t+\Delta t)\\
u(t+\Delta t)=&
u(t)+\Delta t\cdot\dot{u}(t)+\frac{(\Delta t)^2}{3}\cdot\ddot{u}(t)+\frac{(\Delta t)^2}{6}\cdot\ddot{u}(t+\Delta t)
\end{align}
運動方程式の解法：平均加速度法
変位
時刻 $t+\Delta t$ での変位 $u$ を Taylor 展開し， $\Delta t$ の 2 次項まで考慮すると，以下の式が得られる．
\begin{align}
u(t+\Delta t)&=u(t)+\frac{\Delta t}{1!}\cdot\dot{u}(t)+\frac{(\Delta t)^2}{2!}\cdot\ddot{u}(t)+\cdots \\
&=u(t)+\Delta t\cdot\dot{u}(t)+\frac{(\Delta t)^2}{4}\cdot\ddot{u}(t)+\frac{(\Delta t)^2}{4}\cdot\ddot{u}(t+\Delta t)
\end{align}
平均加速度法では， $\Delta t$ の 2 次項を以下のように線形化して上式を得ている．
\begin{equation}
\ddot{u}(t)=\frac{\ddot{u}(t+\Delta t)+\ddot{u}(t)}{2}
\end{equation}
速度
線形加速度法と同様に以下の式を得る．
\begin{equation}
\dot{u}(t+\Delta t)=\dot{u}(t)+\int_t^{t+\Delta t}\ddot{u}(t)dt
=\dot{u}(t)+\frac{\Delta t}{2}\cdot\left(\ddot{u}(t+\Delta t)+\ddot{u}(t)\right)
\end{equation}
加速度
これまでにもとめた変位・速度を運動方程式に代入することにより加速度が以下の通り求まる．
\begin{equation}
\ddot{u}(t+\Delta t)=
\cfrac{f(t+\Delta t)-c\cdot\left(\dot{u}(t)+\cfrac{\Delta t}{2}\cdot\ddot{u}(t)\right)-k\cdot\left(u(t)+\Delta t\cdot\dot{u}(t)+\cfrac{(\Delta t)^2}{4}\cdot\ddot{u}(t)\right)}
{m+c\cdot\cfrac{\Delta t}{2}+k\cdot\cfrac{(\Delta t)^2}{4}}
\end{equation}
平均加速度法まとめ
\begin{align}
\ddot{u}(t+\Delta t)=&
\cfrac{f(t+\Delta t)-c\cdot\left(\dot{u}(t)+\cfrac{\Delta t}{2}\cdot\ddot{u}(t)\right)-k\cdot\left(u(t)+\Delta t\cdot\dot{u}(t)+\cfrac{(\Delta t)^2}{4}\cdot\ddot{u}(t)\right)}
{m+c\cdot\cfrac{\Delta t}{2}+k\cdot\cfrac{(\Delta t)^2}{4}}\\
\dot{u}(t+\Delta t)=&
\dot{u}(t)+\frac{\Delta t}{2}\cdot\ddot{u}(t)+\frac{\Delta t}{2}\cdot\ddot{u}(t+\Delta t)\\
u(t+\Delta t)=&
u(t)+\Delta t\cdot\dot{u}(t)+\frac{(\Delta t)^2}{4}\cdot\ddot{u}(t)+\frac{(\Delta t)^2}{4}\cdot\ddot{u}(t+\Delta t)
\end{align}
運動方程式の解法：Nermark の β 法
計算式
線形加速度法を一般化した方法である． 時刻 $t+\Delta t$ での変位 $u$ および速度 $\dot{u}$ を Taylor 展開したものを以下に示す．
\begin{align}
u(t+\Delta t)&=u(t)+\frac{\Delta t}{1!}\cdot\dot{u}(t)+\frac{(\Delta t)^2}{2!}\cdot\ddot{u}(t)+\frac{(\Delta t)^3}{3!}\cdot\dddot{u}(t)+\cdots \\
\dot{u}(t+\Delta t)&=\dot{u}(t)+\frac{\Delta t}{1!}\cdot\ddot{u}(t)+\frac{(\Delta t)^2}{2!}\cdot\dddot{u}(t)+\cdots
\end{align}
ここで，変位については右辺第 4 項において $1/3!=\beta$ とおくことにより，速度については右辺第 3 項において $1/2!=\gamma$ とおき，双方で高次項を無視することにより以下の式を得る．
\begin{align}
u(t+\Delta t)&=u(t)+\Delta t\cdot\dot{u}(t)+\frac{(\Delta t)^2}{2}\cdot\ddot{u}(t)+\beta\cdot(\Delta t)^3\cdot\dddot{u}(t) \\
\dot{u}(t+\Delta t)&=\dot{u}(t)+\Delta t\cdot\ddot{u}(t)+\gamma\cdot(\Delta t)^2\cdot\dddot{u}(t)
\end{align}
次に，線形加速度法と同様に， $\dddot{u}$ を以下のように線形化する．
\begin{equation}
\dddot{u}(t)=\frac{\ddot{u}(t+\Delta t)-\ddot{u}(t)}{\Delta t}
\end{equation}
上記関係を用いて，運動方程式を整理することにより，以下の方程式が得られる．
\begin{align}
u(t+\Delta t)&=u(t)+\Delta t\cdot\dot{u}(t)+\left(\frac{1}{2}-\beta\right)(\Delta t)^2\cdot\ddot{u}(t)+\beta(\Delta t)^2\cdot\ddot{u}(t+\Delta t) \\
\dot{u}(t+\Delta t)&=\dot{u}(t)+(1-\gamma)\cdot\Delta t\cdot\ddot{u}(t)+\gamma\cdot\Delta t\cdot\ddot{u}(t+\Delta t)
\end{align}
ここで通常は， $\gamma=1/2$ が用いられることを考慮すると，Newmark の β 法は，以下の式で表現できる．
Newmark の β 法まとめ
\begin{align}
\ddot{u}(t+\Delta t)=&
\cfrac{f(t+\Delta t)-c\cdot\left(\dot{u}(t)+\cfrac{\Delta t}{2}\cdot\ddot{u}(t)\right)-k\cdot\left(u(t)+\Delta t\cdot\dot{u}(t)+\left(\cfrac{1}{2}-\beta\right)\cdot(\Delta t)^2\cdot\ddot{u}(t)\right)}
{m+c\cdot\cfrac{\Delta t}{2}+k\cdot\beta\cdot(\Delta t)^2}\\
\dot{u}(t+\Delta t)=&
\dot{u}(t)+\frac{\Delta t}{2}\cdot\ddot{u}(t)+\frac{\Delta t}{2}\cdot\ddot{u}(t+\Delta t)\\
u(t+\Delta t)=&
u(t)+\Delta t\cdot\dot{u}(t)+\left(\cfrac{1}{2}-\beta\right)\cdot(\Delta t)^2\cdot\ddot{u}(t)+\beta\cdot(\Delta t)^2\cdot\ddot{u}(t+\Delta t)
\end{align}
ここに，平均加速度法： $\beta=\cfrac{1}{4} \quad$，線形加速度法： $\beta=\cfrac{1}{6} \quad$ である．
解の安定性
非減衰振動に対し，Newmark の β 法の安定条件は，以下のとおり表される．
\begin{equation}
\gamma\geqq\frac{1}{2} \qquad\qquad \beta\leqq\frac{1}{2} \qquad\qquad \frac{\Delta t}{T_{min}}\leqq\frac{1}{2\pi\sqrt{\gamma/2-\beta}}
\end{equation}
ここに， $T_{min}$ は，構造物の最小固有周期である．
また無条件安定条件は，以下のとおりである．
\begin{equation}
2\beta\geqq\gamma\geqq\frac{1}{2}
\end{equation}
ここで， $\gamma$ が 1/2 を超えると，誤差が発生することが知られており，通常 $\gamma=1/2$ が採用される．
平均加速度法
平均加速度法では， $\gamma=1/2$, $\beta=1/4$ なので，上式の条件を満たし，無条件安定となる．
線形加速度法
線形加速度法においては， $\gamma=1/2$, $\beta=1/6$なので，条件付安定となる．その条件は，以下のとおり．
\begin{equation}
\frac{\Delta t}{T_{min}}\leqq\frac{1}{2\pi\sqrt{\gamma/2-\beta}}=0.5513
\end{equation}
よって，時間間隔を $\Delta t=0.01$ (sec) とすれば $T_{min}\geqq 0.018$ (sec) が安定条件となる． 通常，地震応答スペクトルを求める場合は，地震動の観測時間間隔は 0.01(sec) であり，固有周期の計算は 0.02(sec) より開始するので，安定条件を満たす．
しかし FEM など多自由度系の解析では，系の最小固有周期が 0.018(sec) より小さくなることも考えられるため，線形加速度法では解が発散する可能性がある． このため，多自由度系の解析では，無条件安定である平均加速度法を用いるほうが有利と思われる．
応答スペクトル
加速度応答スペクトル
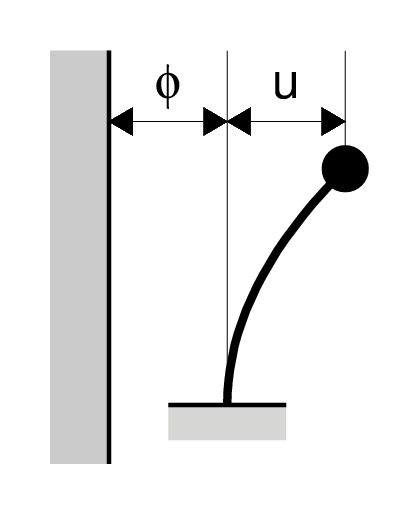
地盤の上に構築された1質点系が，地盤から加速度を受ける場合の運動方程式は以下のとおりとなる．
\begin{equation}
m\cdot(\ddot{\phi}+\ddot{u})+c\cdot\dot{u}+k\cdot u=0
\end{equation}
上式において，質点系に作用する加速度は，地盤に作用する加速度 $\ddot{\phi}$ と構造系内の基準点に対する加速度 $\ddot{u}$ の合計となる． これに対し，質点の運動を減衰させようとする力および変形したバネが元に戻ろうとする力は，構造物内の基準点に対する速度 $\dot{u}$ および変位 $u$ により表され，地盤の変位とは無関係である．
応答スペクトルは，地震動の特性を把握するために用いられるものであり，ある地盤加速度を 1 質点系に与えた時の質点系の 絶対加速度 $\ddot{\phi}+\ddot{u}$ ，相対変位 $\dot{u}$ あるいは相対変位 $u$ の最大値を，質点系の固有周期あるいは固有振動数との関係で整理したグラフとして表現される． 解くべき運動方程式は，基本式を質点の質量$m$で除し，地盤加速度項を右辺に移項した以下の形のものが一般に用いられる．
\begin{equation}
\ddot{u}+2\cdot h\cdot\omega_0\cdot\dot{u}+\omega_0^2\cdot u=-\ddot{\phi}
\end{equation}
ここに， $h$：系の減衰定数， $\omega_0$ ：系の固有円振動数であり，質点の質量 $m$ や減衰係数 $c$ ，バネ定数 $k$ などと以下の関係を有する．
\begin{equation}
c=2\cdot h\sqrt{k\cdot m} \qquad \omega_0=\sqrt{\cfrac{k}{m}} \qquad T=\cfrac{2\pi}{\omega_0}=2\pi\sqrt{\cfrac{m}{k}}
\end{equation}
上記 $T$ は系の固有周期である．
ここでは，地盤加速度を入力値として，加速度応答スペクトルを計算するプログラムを考える．
運動方程式としては一般的な構造物の動的応答解析に用いることを考慮して以下に示す一般形を用い，入力値を地盤加速度 $\ddot{\phi}$ ，減衰定数 $h$ ，固有周期 $T$ とするため，以下の関係を導入する．
\begin{gather}
m\cdot\ddot{u}+c\cdot\dot{u}+k\cdot u=-m\cdot\ddot{\phi}\\
m=1 \qquad k=\frac{4\pi^2\cdot m}{T^2} \qquad c=2\cdot h \sqrt{k\cdot m}
\end{gather}
地盤加速度を $\Delta t$ ピッチで与えるとすると，実際の適用を考え，固有周期は $T=2\cdot\Delta t\sim 10$ (sec)の範囲とし，減衰定数は $h=0.05$ とする．
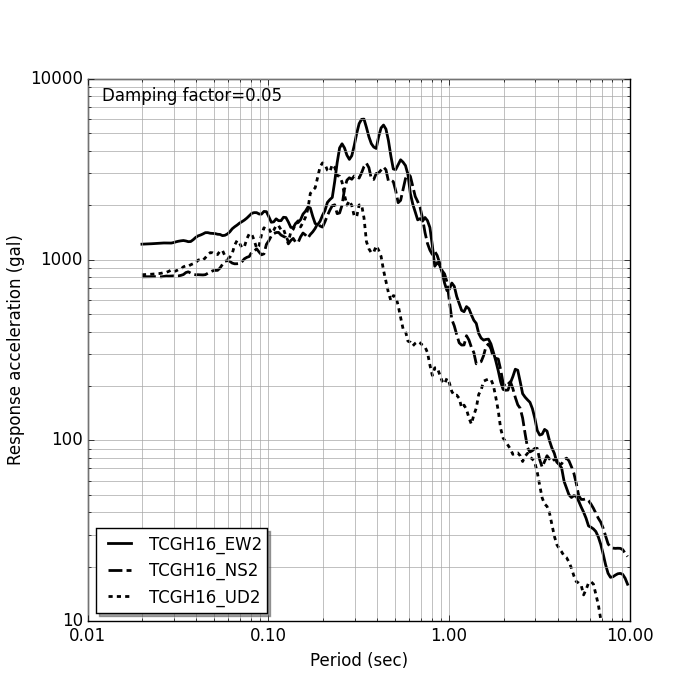
なお，応答スペクトル図を作成する場合の注意点は，応答加速度としては「絶対加速度 $\ddot{u}+\ddot{\phi}$ 」の絶対値の最大を検索・出力することである． すなわち，運動方程式を解いた場合，相対加速度として $\ddot{u}$ が求まるが，応答スペクトルを作成する加速度としては，これに地盤加速度 $\ddot{\phi}$ を加えた加速度を用いることに注意する．
3重応答スペクトル
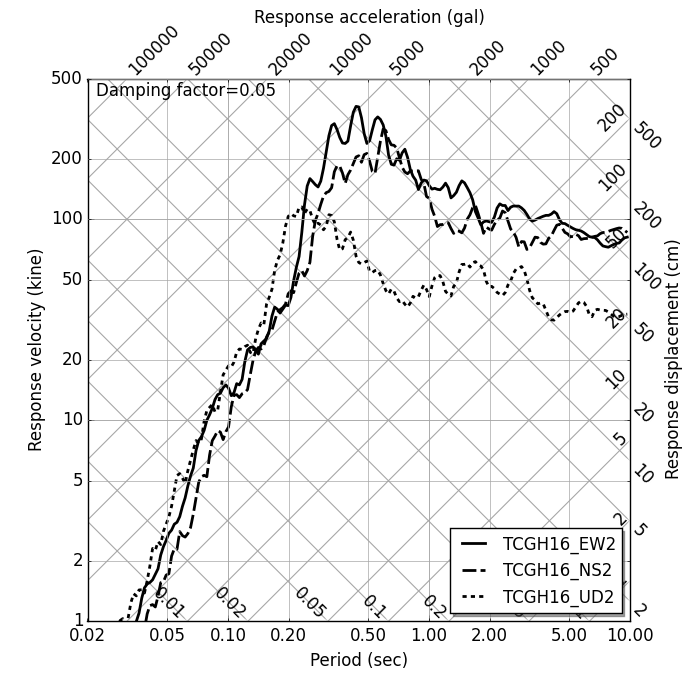
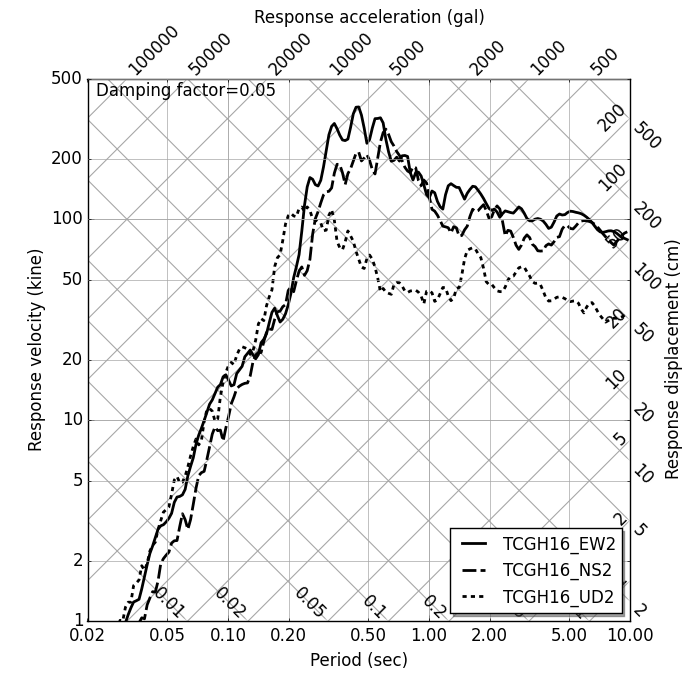
3重応答スペクトルは，速度応答スペクトル図を基本に，加速度軸および変位軸を加えたものである． 近似的にではあるが，1 枚のグラフで加速度・速度・変位の応答地を示すことができる．
加速度軸および変位軸は，以下の関係を用いて定められている．
\begin{equation}
S_a\doteqdot\cfrac{2 \pi}{T}\cdot S_v \qquad\qquad S_d\doteqdot\cfrac{T}{2 \pi}\cdot S_v
\end{equation}
| ここに， | $S_a$ | : 最大絶対加速度応答 |
| $S_v$ | : 最大相対速度応答 | |
| $S_d$ | : 最大相対変位応答 |
 |
 |
 |
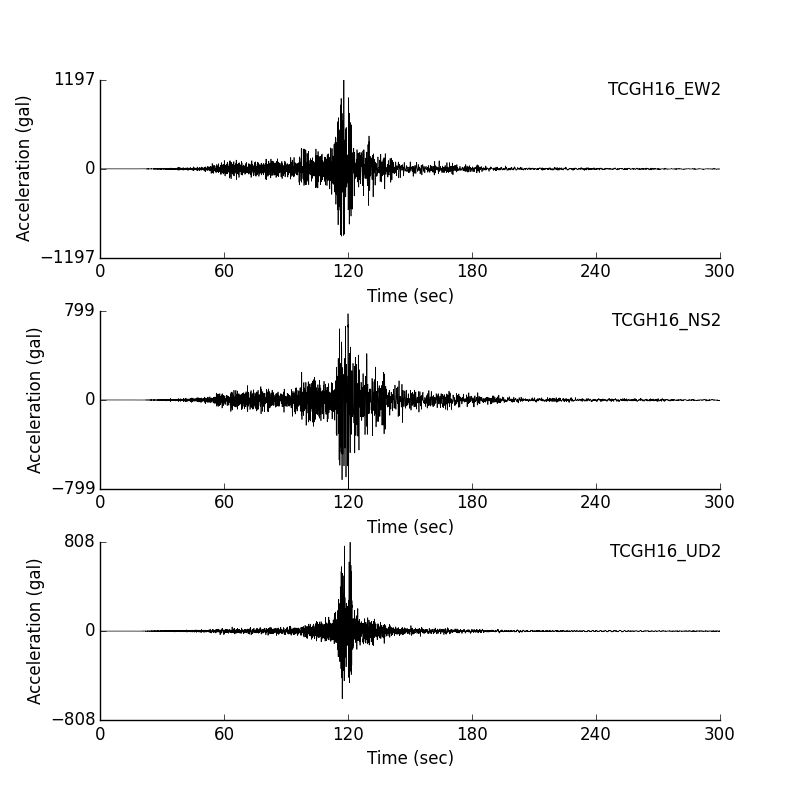
| Input wave time history (ground acceleration) |
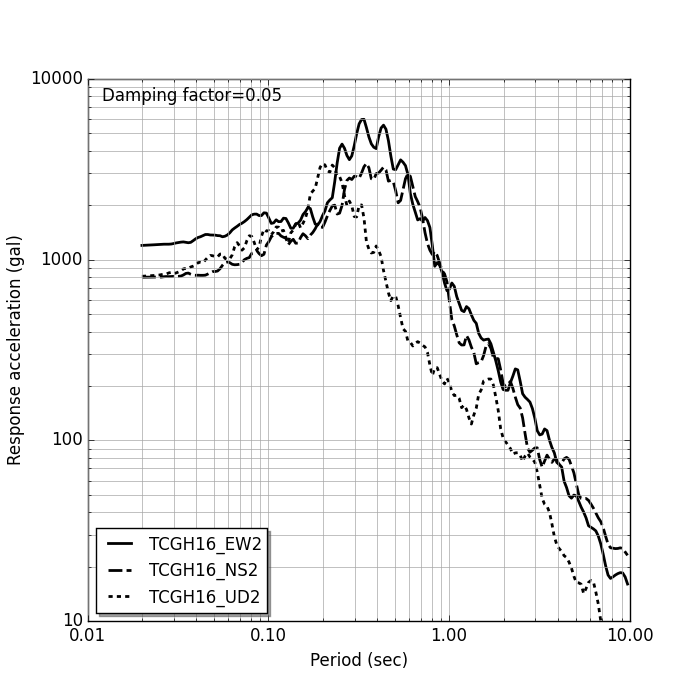
Acceleration response spectrum by Linear acceleration method |
Tripartite response spectrum by Linear acceleration method |
|---|
上図は，(独)防災科学技術研究所が運営している KiK-net のデジタル波形データを用いて描画した入力地震加速度，加速度応答スペクトル，3 重応答スペクトルである． 加速度応答スペクトル，3 重応答スペクトルの描画ベースとなる速度応答スペクトルは，線形加速度法により計算したものである． また，入力加速度は基線補正を行っている．基線補正の方法は，大崎順彦著「新・地震動のスペクトル解析入門」に掲載の方法によっている．
フーリエスペクトル
有限フーリエ係数
時刻に関する連続関数 $x(t)$ について，以下の時刻歴データがあるものとする．
| 標本数 | $N$ |
| 標本点間隔 | $\Delta t$ |
| 標本値 | $x_m \qquad m=0,1,2,\cdots,N-1$ |
標本数 $N$ は高速フーリエ変換を適用することを前提に $N=2^L$（ $L$ は正の整数）とし， 標本値 $x_m$ を $k=N/2$ までの有限三角級数で表せるものとすれば，以下の式が得られる．
\begin{align}
x_m=&\sum_{k=0}^{N/2}\left\{A_k\cdot\cos\left(\frac{2\pi k}{N\cdot\Delta t}\cdot t\right)+B_k\cdot\sin\left(\frac{2\pi k}{N\cdot\Delta t}\cdot t\right)\right\} \\
=&\frac{A_0}{2}+\sum_{k=1}^{N/2-1}\left(A_k\cdot\cos\frac{2\pi k m}{N}+B_k\cdot\sin\frac{2\pi k m}{N}\right)+\frac{A_{n/2}}{2}\cdot\cos\frac{2\pi(N/2)m}{N}
\end{align}
\begin{equation}
m=0,1,2,\cdots,N-1 \qquad t=m\cdot\Delta t
\end{equation}
上式を，関数 $x(t)$ の有限フーリエ近似，係数 $A_k, B_k$ を有限フーリエ係数という． また，有限フーリエ係数を求める演算をフーリエ変換 (Fourier transform)， 有限フーリエ係数が既知で元の標本値を再現する演算をフーリエ逆変換 (Fourier inverse transform) という．
\begin{align}
A_k=&\frac{2}{N}\sum_{m=0}^{N-1}x_m\cdot\cos\frac{2\pi k m}{N} & \qquad & k=0,1,2,\cdots,N/2-1,N/2 \\
B_k=&\frac{2}{N}\sum_{m=0}^{N-1}x_m\cdot\sin\frac{2\pi k m}{N} & \qquad & k=1,2,\cdots,N/2-1
\end{align}
\begin{equation}
\frac{A_0}{2}=\frac{1}{N}\sum_{m=0}^{N-1}x_m \qquad \text{(全標本値の平均)}
\end{equation}
有限フーリエ変換の複素数表示
オイラーの公式（ $e^{\pm i\theta}=\cos\theta \pm i\sin\theta$ ）により複素数表示を行う．
\begin{align*}
&\text{フーリエ変換} &C_k=&\frac{1}{N}\sum_{m=0}^{N-1}x_m\cdot e^{-i(2\pi k m/N)} & k=&0,1,2,\cdots,N-1 \\
&\text{フーリエ逆変換}&x_m=&\sum_{k=0}^{N-1}C_k\cdot e^{+i(2\pi k m/N)} & m=&0,1,2,\cdots,N-1
\end{align*}
フーリエ係数と複素フーリエ係数の関係
\begin{equation*}
C_k=\frac{A_k-i B_k}{2} \qquad A_k+i B_k=A_{N-k}-i B_{N-k}
\end{equation*}
\begin{equation*}
A_k=2\cdot Re(C_k) \qquad B_k=-2\cdot Im(C_k) \qquad k=0,1,2,\cdots,N/2
\end{equation*}
フーリエ振幅スペクトル，フーリエ位相スペクトル
\begin{align*}
&\text{振動数} &~&f_k =\frac{k}{N\cdot\Delta t} \qquad k=0,1,2,\cdots,N/2 \\
&\text{フーリエ振幅}& &F_k =\frac{N\cdot\Delta t}{2}\sqrt{A_k{}^2+B_k{}^2}=N\cdot\Delta t|C_k|=N\cdot\Delta t\sqrt{Re(C_k)^2+Im(C_k)^2} \\
&\text{位相角} & &\phi_k =\arctan\left(-\frac{B_k}{A_k}\right)=\arctan\left(\frac{Im(C_k)}{Re(C_k)}\right) \qquad (-\pi<\phi_k<\pi) \\
&\text{位相波} & &\hat{x}(t)=\sum_{k=1}^{N/2}\cos(2\pi\cdot f_k \cdot t+\phi_k)
\end{align*}
フーリエ振幅を振動数に対してプロットしたものをフーリエ振幅スペクトル(単にフーリエスペクトルともいう)，位相角を振動数に対してプロットしたものをフーリエ位相スペクトルという．
簡単なフーリエ変換・逆変換の事例
以下に簡単な Fourier 変換・逆変換の結果を示す．
- データ（data）は Fortran90 の乱数発生サブルーチン random_number を用いて 16 個の一様乱数を発生させたものである．データの並び順は発生させた乱数の順番である．
- Re(Ck) および Im(Ck) は，これを FFT にかけて複素フーリエ係数を求めたものである．
- abs(Ck) は複素フーリエ係数の絶対値，fp(Ck) は位相角である．
- Re(xm) および Im(xm) は，上記で求めた複素フーリエ係数を逆変換して，入力データの再現を行ったものである．
| i | data | Re(Ck) | Im(Ck) | abs(Ck) | fp(Ck) | Re(xm) | Im(xm) |
|---|---|---|---|---|---|---|---|
| 1 | 0.998 | 0.478 | 0.000 | 0.478 | 0.000 | 0.998 | 0.000 |
| 2 | 0.567 | 0.154 | -0.014 | 0.154 | -5.171 | 0.567 | 0.000 |
| 3 | 0.966 | -0.003 | -0.053 | 0.053 | -93.070 | 0.966 | 0.000 |
| 4 | 0.748 | -0.018 | -0.008 | 0.020 | -155.386 | 0.748 | 0.000 |
| 5 | 0.367 | 0.057 | -0.014 | 0.059 | -14.125 | 0.367 | 0.000 |
| 6 | 0.481 | 0.000 | 0.092 | 0.092 | 89.861 | 0.481 | 0.000 |
| 7 | 0.074 | 0.012 | 0.030 | 0.033 | 67.645 | 0.074 | 0.000 |
| 8 | 0.005 | 0.027 | -0.047 | 0.054 | -60.520 | 0.005 | 0.000 |
| 9 | 0.347 | 0.062 | 0.000 | 0.062 | 0.000 | 0.347 | 0.000 |
| 10 | 0.342 | 0.027 | 0.047 | 0.054 | 60.520 | 0.342 | 0.000 |
| 11 | 0.218 | 0.012 | -0.030 | 0.033 | -67.645 | 0.218 | 0.000 |
| 12 | 0.133 | 0.000 | -0.092 | 0.092 | -89.861 | 0.133 | 0.000 |
| 13 | 0.901 | 0.057 | 0.014 | 0.059 | 14.125 | 0.901 | 0.000 |
| 14 | 0.387 | -0.018 | 0.008 | 0.020 | 155.386 | 0.387 | 0.000 |
| 15 | 0.445 | -0.003 | 0.053 | 0.053 | 93.070 | 0.445 | 0.000 |
| 16 | 0.662 | 0.154 | 0.014 | 0.154 | 5.171 | 0.662 | 0.000 |
| Ave. | 0.478 |
上表より以下のことがわかり，理屈どおりの結果となっている．
- フーリエ複素係数実数部は，最初の項 (i=1) は入力全データの平均値となっている．また入力データ数を n 個とすれば n/2+1 (i=9) を中心に対称の分布をしている．
- フーリエ複素係数虚数部は，最初の項 (i=1) は 0 となっている．また入力データ数を n 個とすれば n/2+1 (i=9) を中心に符号が逆転した対称の分布をしている．
- フーリエ逆変換の結果は，実数部は入力データを再現しており，虚数部は誤差の範囲で全て 0 となっている．
ここでは南茂夫先生の「科学計測のための波形データ処理 計測システムにおけるマイコン／パソコン活用技術」に掲載されている実数演算による BASIC プログラムを，Fortran90 に書き換えたプログラムを用いている．
このプログラムの使用上の注意点は以下のとおり．
- フーリエ変換時 複素フーリエ係数 $C_k=\frac{1}{N}\sum_{m=0}^{N-1}x_m\cdot e^{-i(2\pi k m/N)}$ の $\sum_{m=0}^{N-1}x_m\cdot e^{-i(2\pi k m/N)}$ の部分を出力するため，実際のフーリエ複素係数とするためには出力値をデータ数 $N$ で除す必要がある．
- フーリエ逆変換時 与えられたフーリエ複素係数から，逆変換して加速度値を求めるためには，フーリエ変換とフーリエ逆変換の式の指数部を比較して判るように，虚数部の符号を逆転させて入力する必要があることに注意する．
フーリエスペクトル出力事例
フーリエスペクトルを描画する際は，以下の関係を描画する．
\begin{align*}
&\text{振動数} &~&f_k=\frac{k}{N\cdot\Delta t} & (k=0\sim N/2)\\
&\text{フーリエ振幅}&~&F_k=N\cdot\Delta t\sqrt{Re(C_k)^2+Im(C_k)^2} & (k=0\sim N/2)
\end{align*}
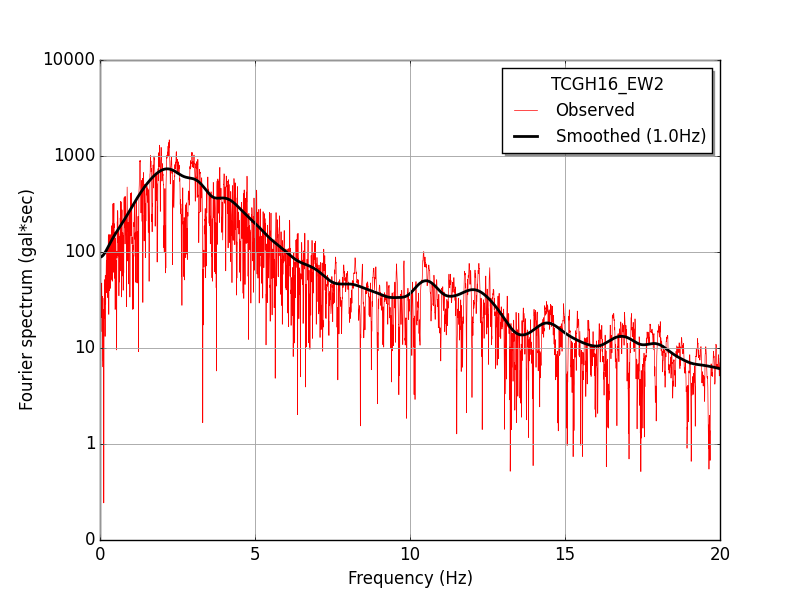
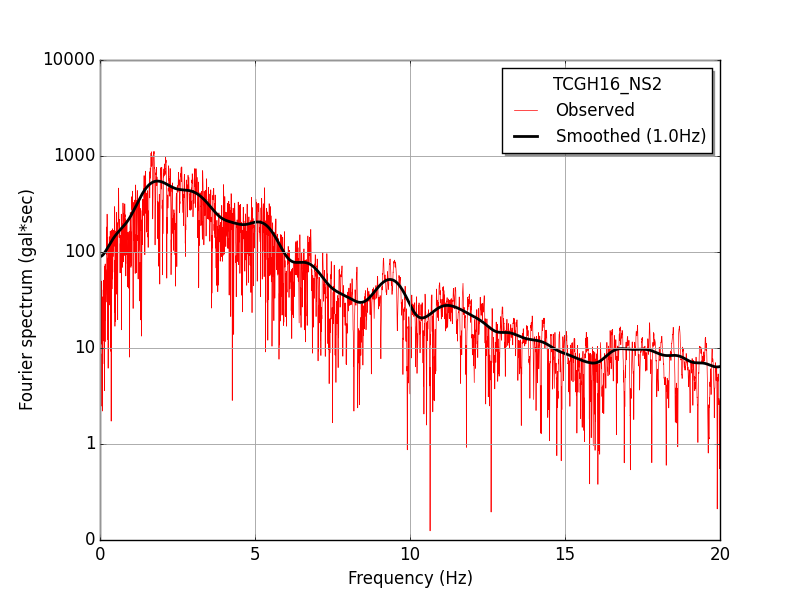
下図は，線形加速度法での計算に用いた地震動加速度時刻歴より計算した，フーリエスペクトルを示したものである． スペクトルの計算値そのもの（細い赤線）では，変化が激しく，振動数のピークを読み取りにくいので，Parzen window による平滑化を行っている．
Parzen winndow による平滑化 subroutine SWIN は大崎順彦先生の著書「新・地震動のスペクトル解析入門」に掲載の FORTRAN ソースを Fortran90 に書き直したものである．
 |
 |
 |
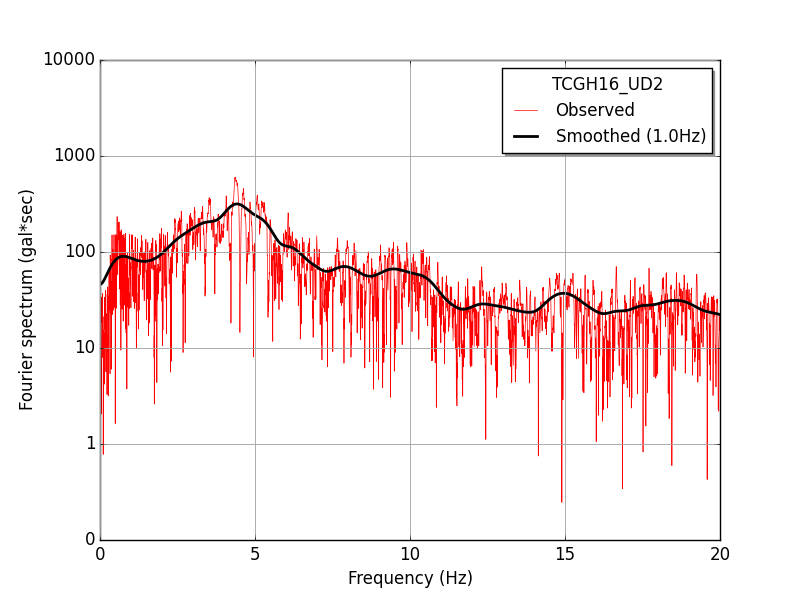| Fourier spectrum (black line: after smoothing, red line: original) | ||
|---|---|---|
模擬地震波作成
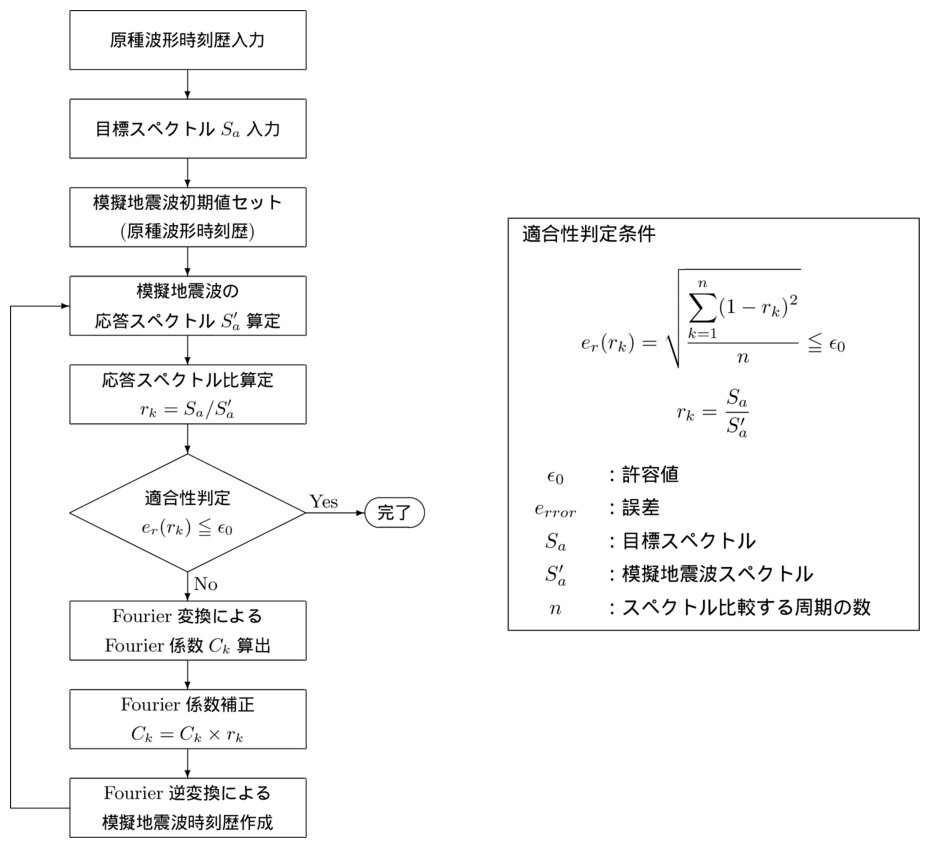
模擬地震波作成処理の考え方
- 基本フローは，「国土技術政策総合研究所資料（国総研資料第244号：平成17年3月）：大規模地震に対するダムの耐震性能照査に関する資料，資料1-6 加速度応答スペクトルに適合する時刻歴波形の作成方法」を参考に作成しています．
- 機能は，目標とする加速度応答スペクトルと位相特性を参照する原種波形時刻歴を入力することにより，目標スペクトルに適合させた模擬地震波を作成するものです．
- 適合の許容誤差は 5% としていますが，収束しない場合もあるので，スペクトル比より計算した誤差が減少傾向から増加に転じた時点で収束計算を打ち切っています．
- 模擬地震波の継続時間は，原種波形と同時刻に始まり同時刻に終了・打ち切っています．
- 目標スペクトルは，周期の関数として数字入力しますが，内部処理では Fourier 変換を行う関係上，周波数の関数として扱っています．
 |
地震継続時間の影響
前出の考え方で作成した模擬地震波作成プログラムを用いて，地震継続時間の影響をテストしてみる．
地震継続時間は，「設計用入力地震動作成手法技術指針(案)，建設省建築研究所・(財)日本建築センター，平成4年3月」を参考に以下の考え方で設定した．
| 設定ケース | 包絡関数 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
 |
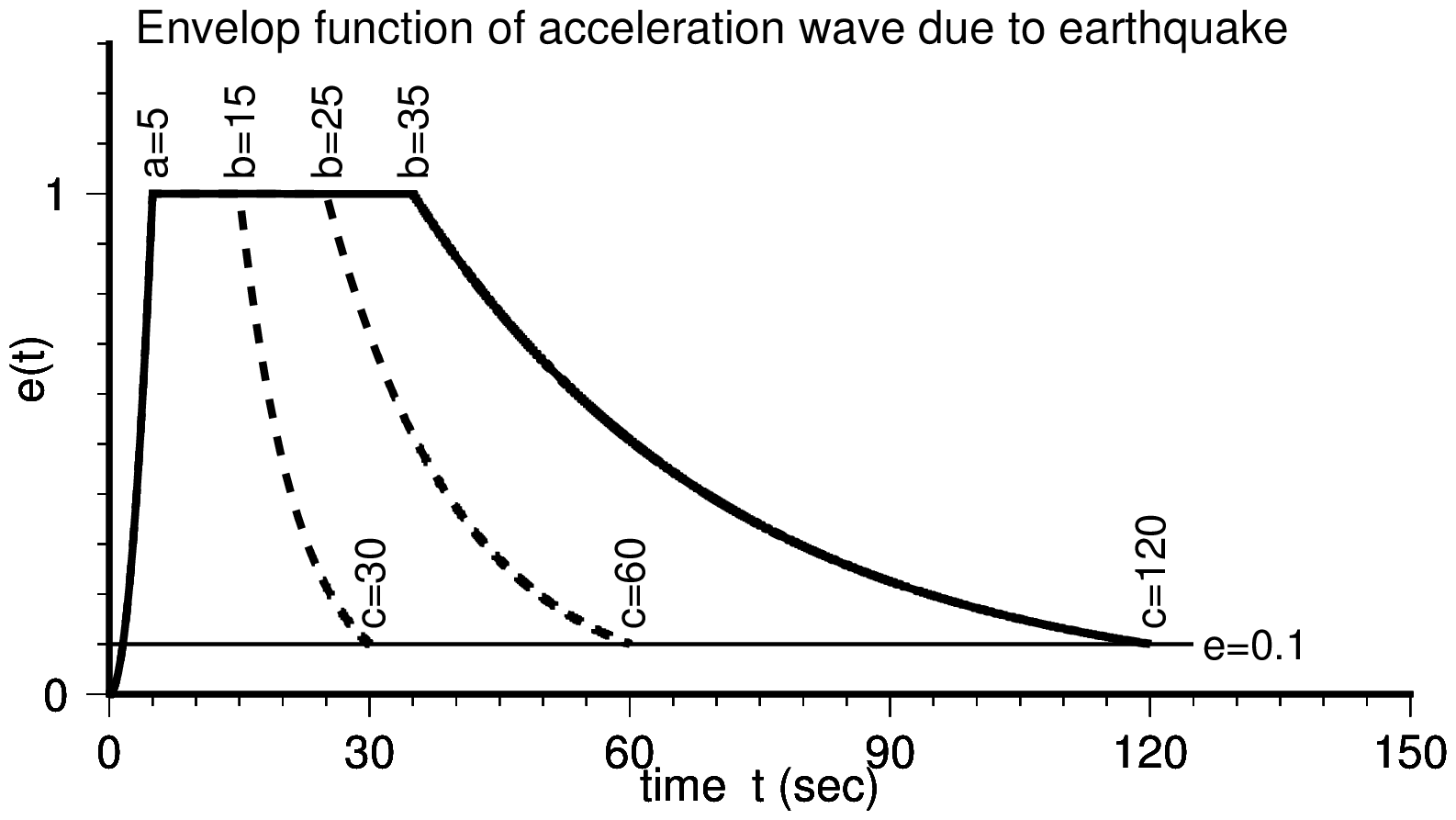| Envelop function |
|---|
テスト用の波形は以下の要領で作成した．
- Fortran90 の random_number により $0\sim 1$ の範囲の一様乱数を必要個数発生させる．
- 上記で得た乱数列の範囲を $-1\sim 1$ に拡張し，これに包絡関数と設定した最大加速度を乗じることによりテスト波形を得る．
- サンプリングピッチは $\Delta t=0.01$ (sec) とする．
- 最大加速度は 100gal とする．
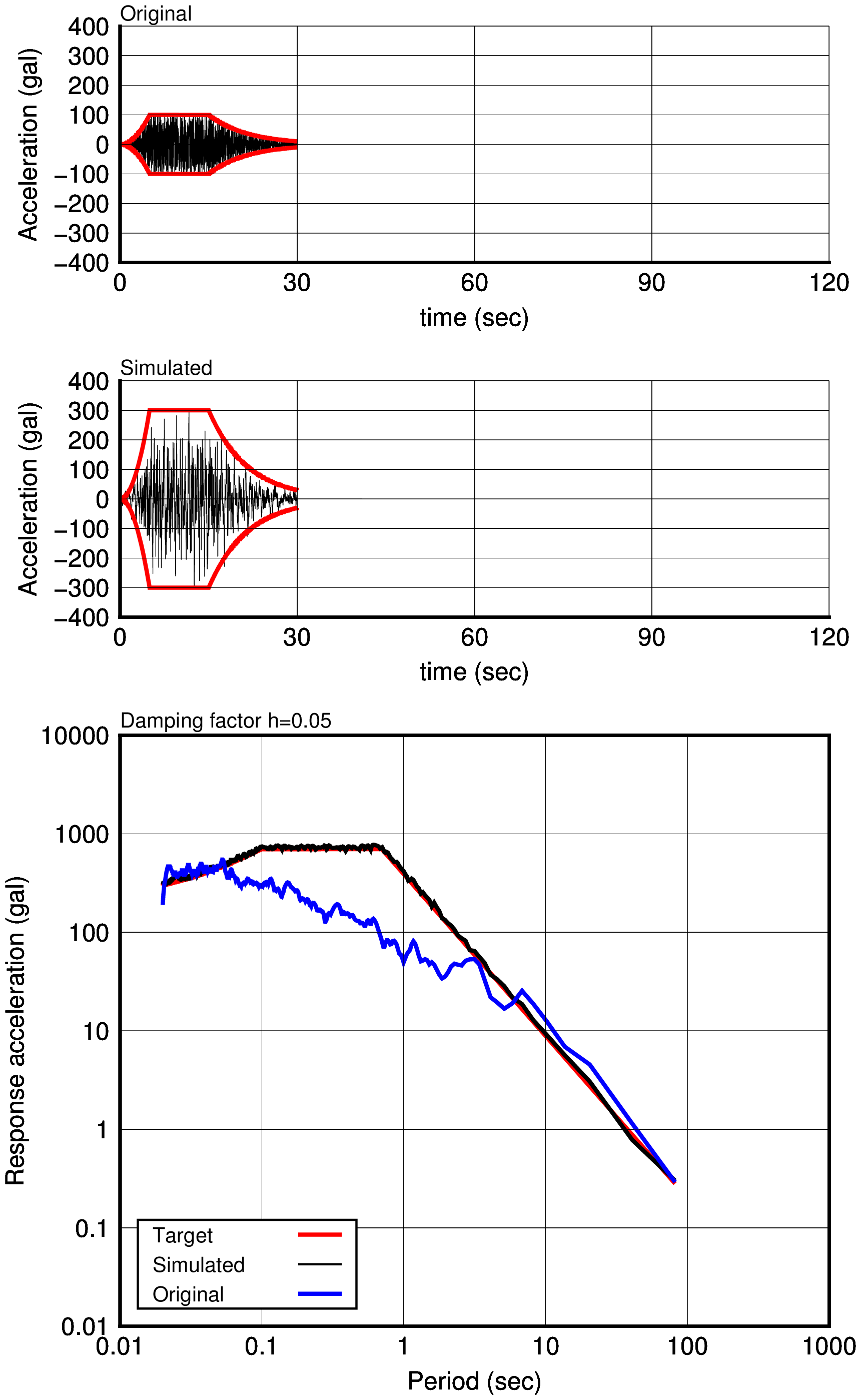
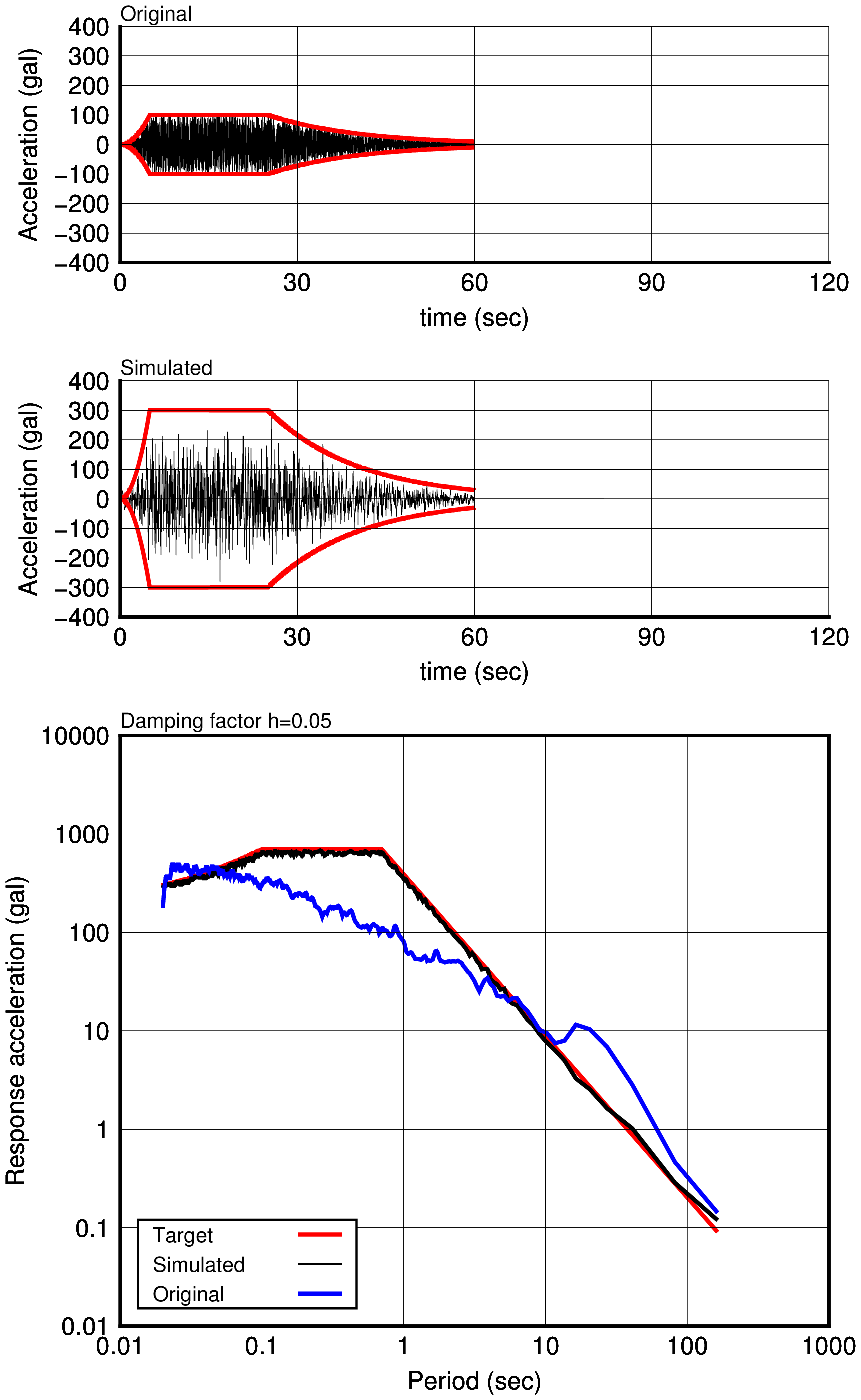
上記で得たテスト波形より，目標スペクトルに適合する模擬波形を作成する． 目標スペクトルにおける最大加速度は，300gal である．
以降に各ケースにおける原種波形，模擬波形，加速度応答スペクトルを示す． なお，実際の耐震解析においては，乱数による位相の使用の是非の議論もあるようであるが，ここでは作成した模擬地震波の特性をつかむ数値実験と割り切り，計算を行っている．
 |
 |
 |
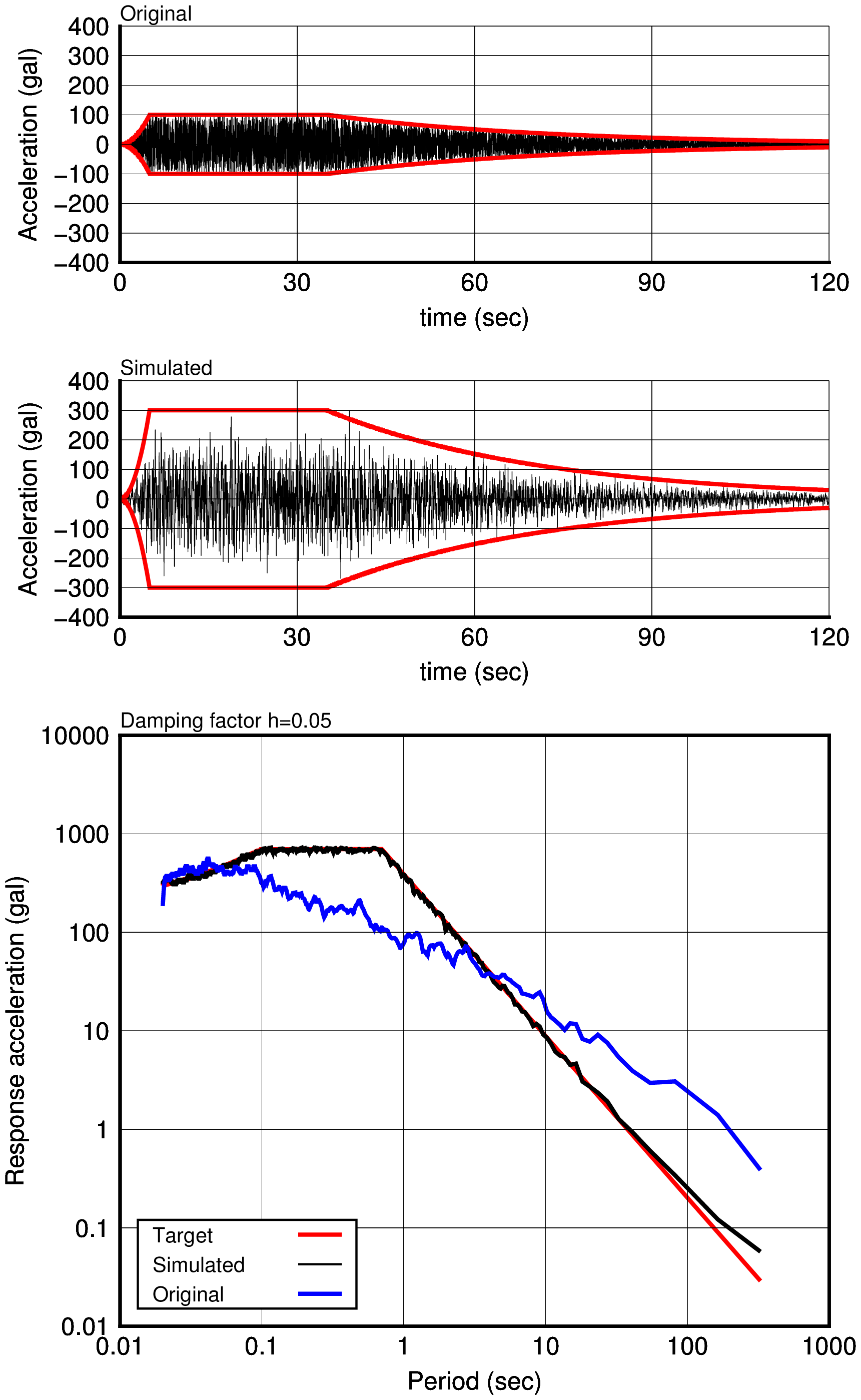| Case-1 (duration time c=30sec) | Case-2 (duration time c=60sec) | Case-3 (duration time c=120sec) |
|---|
位相角について (Case 1 の事例)
- 位相角は，原種波形とこれより作成された模擬地震波で全く等しい．
- すなわち，この方法では原種波形の位相角の情報はそのまま保持され，フーリエ振幅のみを目標スペクトルに整合させるよう変化させていることがわかる．
- 模擬地震波の位相角より作成した位相波時刻歴は，原種波形の時刻歴と似通った形状となっている．
- 上記の理由は不明であるが，位相波には振幅情報は入っていないにもかかわらず，位相波の形状が，継続時間や包絡曲線に大きく影響していると考えることができる．
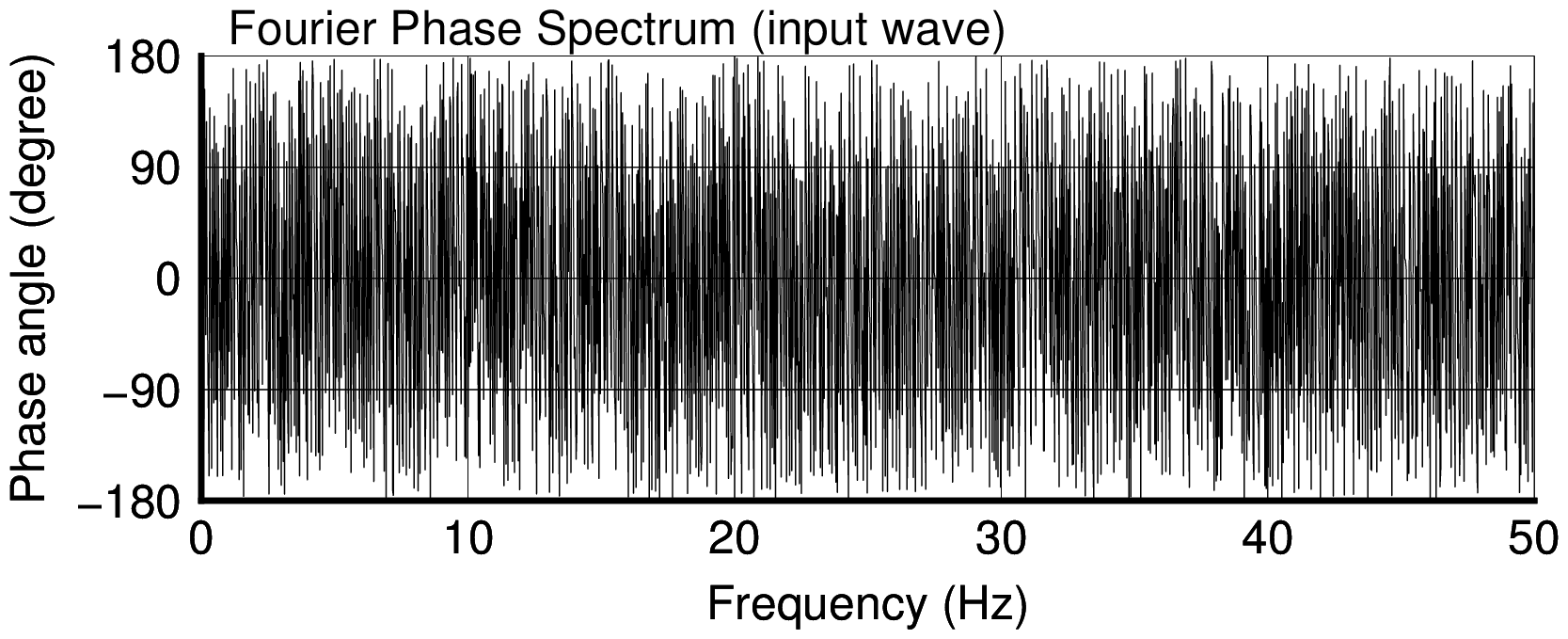 Fourier phase spectrum of input wave |
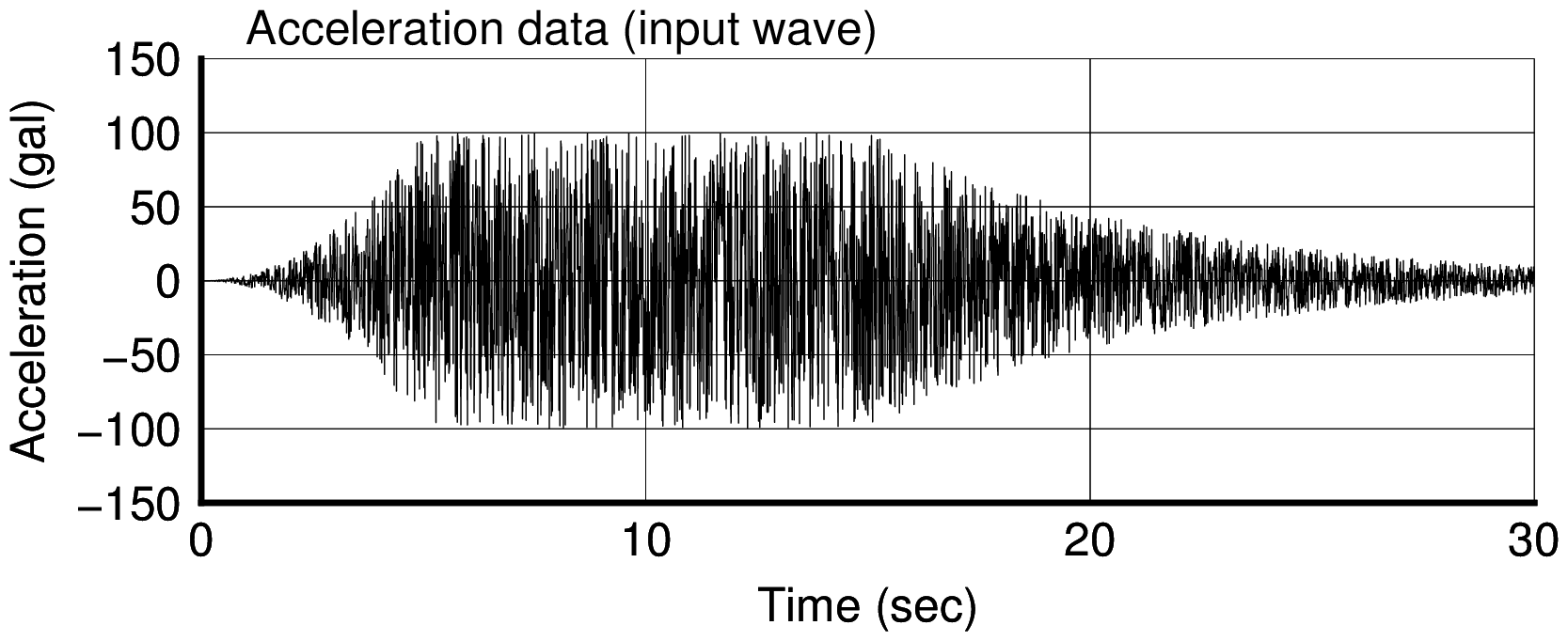 Input wave time history |
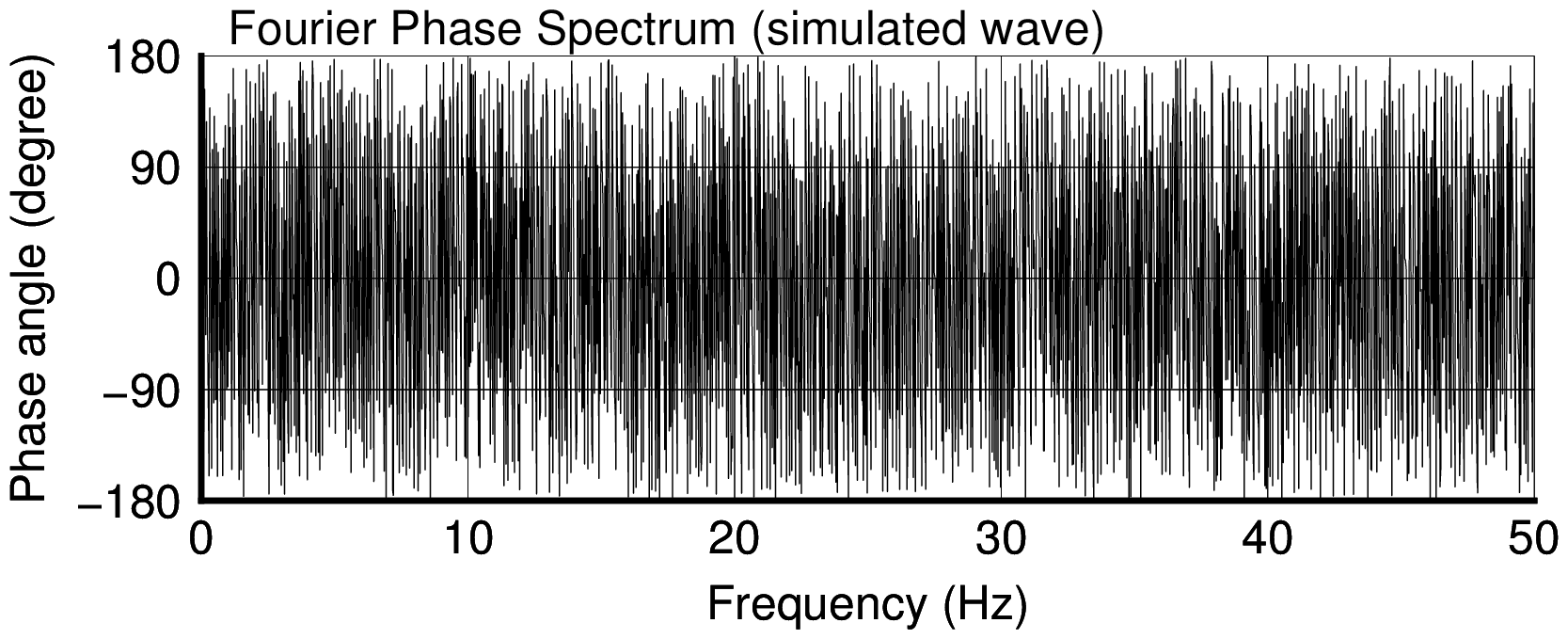 Fourier phase spectrum of simulated wave |
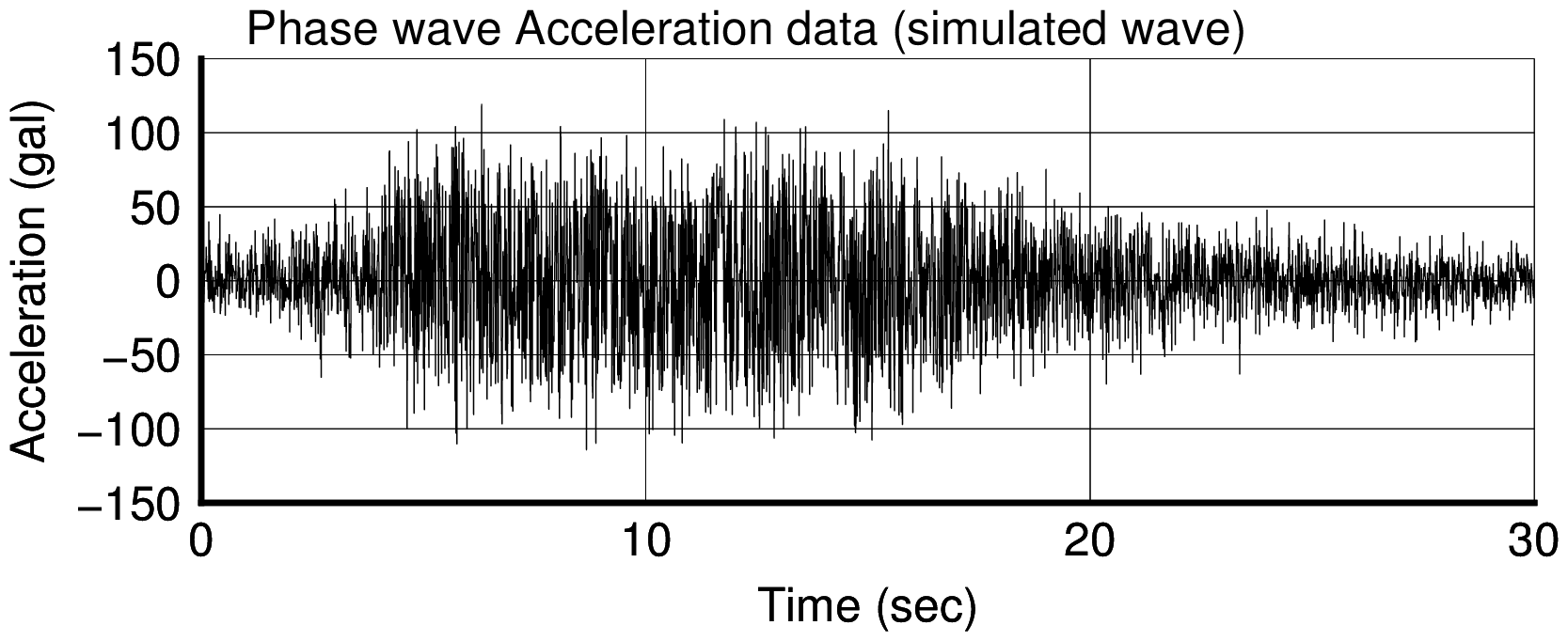 Simulated phase wave time history |
| Sample of Phase wave analysis | |
|---|---|
運動方程式の解法：Runge-Kutta 法
計算式
Runge-Kutta 法を適用するため，1 質点系の運動方程式を，以下のように変形する．
\begin{equation*}
\begin{cases}
\quad f_a(t,x,y)=\dot{x}=\cfrac{dx}{dt}=y \\
\quad \\
\quad f_b(t,x,y)=\ddot{x}=\cfrac{dy}{dt}=\cfrac{f(t)}{m}-\cfrac{c}{m}\cdot y-\cfrac{k}{m}\cdot x
\end{cases}
\end{equation*}
Runge-Kutta 法による計算手順は，以下に示すとおり．ここに $h$ は時間増分である． 変数 $t$, $x$, $y$ のそれぞれに初期値を与えることが必要である．
\begin{equation*}
\begin{cases}
&k_{a1}=f_a(t_n,x_n,y_n) \\
&k_{a2}=f_a(t_n+h/2,x_n+h/2\cdot k_{a1},y_n+h/2\cdot k_{a1}) \\
&k_{a3}=f_a(t_n+h/2,x_n+h/2\cdot k_{a2},y_n+h/2\cdot k_{a2}) \\
&k_{a4}=f_a(t_n+h,x_n+h\cdot k_{a3},y_n+h\cdot k_{a3}) \\
&x_{n+1}=x_n+h/6\cdot (k_{a1}+2k_{a2}+2k_{a3}+k_{a4})
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
&k_{b1}=f_b(t_n,x_n,y_n) \\
&k_{b2}=f_b(t_n+h/2,x_n+h/2\cdot k_{b1},y_n+h/2\cdot k_{b1}) \\
&k_{b3}=f_b(t_n+h/2,x_n+h/2\cdot k_{b2},y_n+h/2\cdot k_{b2}) \\
&k_{b4}=f_b(t_n+h,x_n+h\cdot k_{b3},y_n+h\cdot k_{b3}) \\
&y_{n+1}=y_n+h/6\cdot (k_{b1}+2k_{b2}+2k_{b3}+k_{b4})
\end{cases}
\end{equation*}
\begin{equation*}
\begin{cases}
\quad \ddot{x}=\cfrac{f(t)}{m}-\cfrac{c}{m}\cdot y_{n+1}-\cfrac{k}{m}\cdot x_{n+1} & \text{(acceleration)}\\
\quad \dot{x}=y_{n+1} & \text{(velocity)}\\
\quad x=x_{n+1} & \text{(displacement)}
\end{cases}
\end{equation*}
解の安定性
運動方程式を解く上での Runge-Kutta 法の安定性を検討する． このため，以下に示す単純な運動方程式を考える．
\begin{equation}
\dot{z}=i\cdot\omega\cdot z
\end{equation}
上記方程式は，減衰のない場合の，変位( $z$ )と速度( $\dot{z}$ )の関係を示す部分方程式である．ここに $\omega$ は固有角振動数である． この微分方程式に Runge-Kutta 法を適用する．
\begin{align*}
k_1=&f(z_n) &=&i\omega z \\
k_2=&f(z_n+h/2\cdot k_1)&=&(i\omega-h/2\cdot\omega^2) z_n \\
k_3=&f(z_n+h/2\cdot k_2)&=&(i\omega-h/2\cdot\omega^2-i\cdot h^2/4\cdot\omega^3) z_n \\
k_4=&f(z_n+h \cdot k_2)&=&(i\omega-h \cdot\omega^2-i\cdot h^2/2\cdot\omega^3+h^3/4\cdot\omega^4) z_n
\end{align*}
\begin{align*}
z_{n+1}=&z_n+h/6 (k_1+2k_2+2k_3+k_4) \\
=&z_n\left\{1-\cfrac{1}{2}h^2\omega^2+\cfrac{1}{24}h^4\omega^4+i\left(h\omega-\cfrac{1}{6}h^3\omega^3\right)\right\}\\
=&z_n\left\{1-\cfrac{1}{2}x^2 +\cfrac{1}{24}x^4 +i\left(x -\cfrac{1}{6}x^3 \right)\right\}
\qquad \text{where, $x=h\omega$.}
\end{align*}
上記より，以下の関係が得られる．
\begin{equation*}
\frac{z_{n+1}}{z_n}=\left\{1-\cfrac{1}{2}x^2+\cfrac{1}{24}x^4+i\left(x-\cfrac{1}{6}x^3\right)\right\}=A\cdot e^{i\theta}
\qquad \text{where, $x=h\omega$.}
\end{equation*}
このケースの場合，数値積分の安定性は， $|A|\leqq 1$ であるため，
\begin{equation*}
A^2=\left(1-\cfrac{1}{2}x^2+\cfrac{1}{24}x^4\right)^2+\left(x-\cfrac{1}{6}x^3\right)^2=1+\cfrac{x^6}{576}(x^2-8)\leqq 1
\end{equation*}
\begin{equation*}
x=h\omega\leqq 2\sqrt{2} \quad\Rightarrow\quad h\leqq\cfrac{2\sqrt{2}}{2\pi}T\doteqdot 0.450 T \qquad \text{where, $T$ is a natural period}
\end{equation*}
上記より，もし固有周期が 0.02 秒の構造物の挙動を知りたければ，時間増分は 0.009秒 (0.02 $\times$ 0.45) より小さくとる必要があることに注意が必要である．
計算事例
Runge-Kutta 法の適用事例として，これを用いた応答スペクトル計算を行った． 計算条件は，以下のとおり．
\begin{equation*}
m=1 \qquad k=\frac{4\pi^2 m}{T^2} \qquad c=2h\sqrt{k m}
\end{equation*}
| 地震動入力時間間隔 | $\Delta t=0.01$(sec) |
| 固有周期の範囲 | $T=0.02 \sim 10$(sec) |
| 減衰定数 | $h=0.05$ |
加えて，以下の事項を考慮した．
- 計算結果出力間隔は，入力地震動と同じ 0.01 秒とした．
- Runge-Kutta 法による計算時間間隔は，数値積分の安定性を考慮して地震動入力時間間隔の 1/5 (0.002 秒) とした．
- なぜならば，もし計算時間間隔を地震動入力時間間隔と同じ 0.01 秒とすれば，安定条件が満足できないからである．
- このため，計算においては，入力地震動を指定した時間間隔内で線形内挿している．
計算結果は以下に示すとおりである．
 |
 |
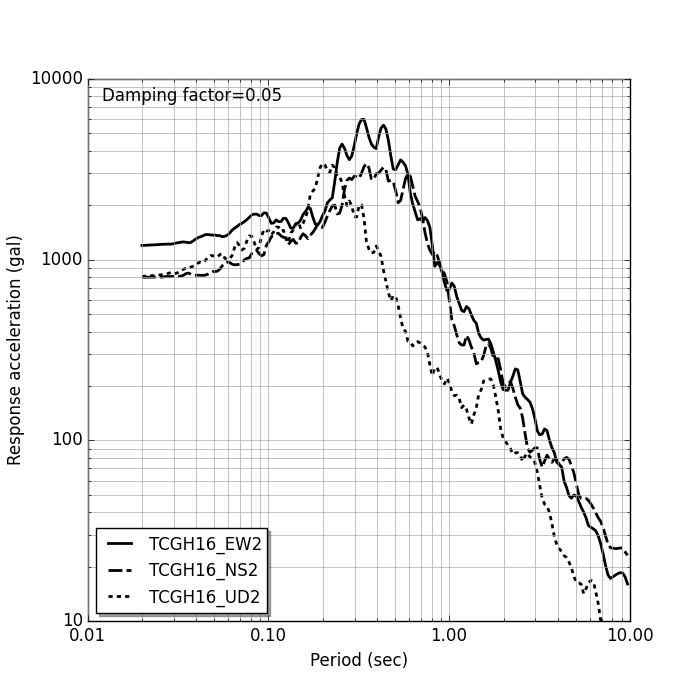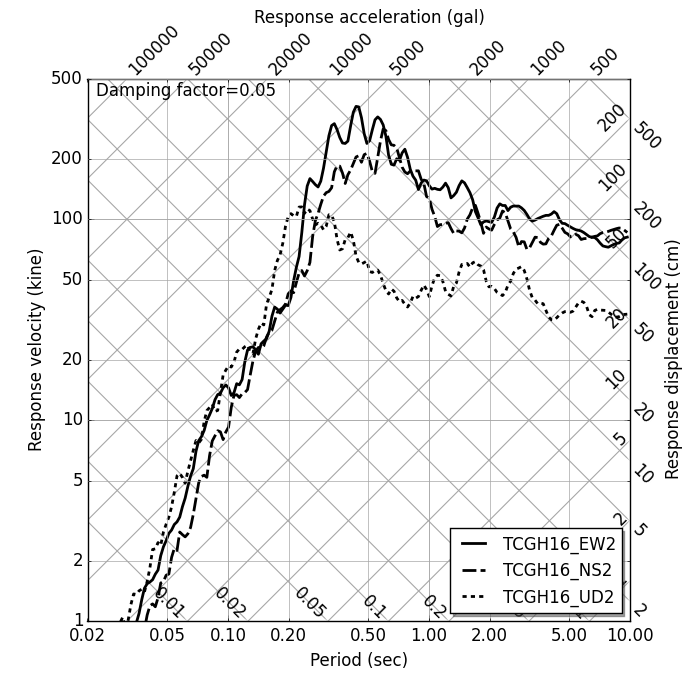| Acceleration response spectrum by Runge-Kutta method |
Tripartite response spectrum by Runge-Kutta method |
|---|
運動方程式の解法：FFT による周波数領域の計算
時刻歴計算法には，時間領域の数値積分によるものと，フーリエ変換・逆変換を活用した周波数領域の計算によるものがある． ここでは，周波数領域の計算による 1 質点系の時刻歴計算法を述べる．
運動方程式は，以下の形式とする．
\begin{equation}
\ddot{u}(t)+2\cdot h\cdot\omega_0\cdot\dot{u}(t)+\omega_0^2\cdot u(t)=-a(t) \label{eq:frq1}
\end{equation}
ここに， $u$ ：質点の相対変位， $a$ ：地盤加速度， $h$ ：系の減衰定数， $\omega_0$ ：系の固有円振動数である．
地盤加速度および質点の変位・速度・加速度をフーリエ逆変換を用いて表すと，
\begin{align}
&a(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}A(\omega) e^{i\omega t}d\omega \\
&u(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}U(\omega) e^{i\omega t}d\omega \\
&\dot{u}(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}i\omega\cdot U(\omega) e^{i\omega t}d\omega \\
&\ddot{u}(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}-\omega^2\cdot U(\omega) e^{i\omega t}d\omega
\end{align}
上式群を，運動方程式に代入することにより，
\begin{align}
&U(\omega)=\frac{A(\omega)}{(\omega^2-\omega_0^2)-2 h \omega_0 \omega\cdot i} \\
&u(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{A(\omega)}{(\omega^2-\omega_0^2)-2 h \omega_0 \omega\cdot i} e^{i\omega t}d\omega \\
&\dot{u}(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{i\omega A(\omega)}{(\omega^2-\omega_0^2)-2 h \omega_0 \omega\cdot i} e^{i\omega t}d\omega \\
&\ddot{u}(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{-\omega^2 A(\omega)}{(\omega^2-\omega_0^2)-2 h \omega_0 \omega\cdot i} e^{i\omega t}d\omega
\end{align}
として，応答値である変位・速度・加速度が表現できる．
ここで，
\begin{equation}
H(\omega)=\frac{1}{(\omega^2-\omega_0^2)-2 h \omega_0 \omega\cdot i}
\end{equation}
は伝達関数あるいは周波数応答関数と呼ばれている．
応答値の計算手順は以下のとおり．
- 入力加速度$a$の複素フーリエ係数 $A(\omega)$ の算出
- 伝達関数 $H(\omega)$ の算出
- $A(\omega)\cdot H(\omega)$ のフーリエ逆変換による変位時刻歴 $u(t)$ の算出
- $i\omega\cdot A(\omega)\cdot H(\omega)$ のフーリエ逆変換による速度時刻歴 $\dot{u}(t)$ の算出
- $-\omega^2\cdot A(\omega)\cdot H(\omega)$ のフーリエ逆変換による加速度時刻歴 $\ddot{u}(t)$ の算出
実際の計算では高速フーリエ変換を用いるため，以下に注意する．
- データ数は有限で $N$ 個（ $N$ は 2 の累乗）とし，データの時間間隔を $\Delta t$ とする．
- 計算される振動数 $f_k$ および円振動数 $\omega$ は以下のとおりとなる．ここでデータは $N$ 個あるが実態としての振動数は $N/2+1$ 個しか定義できないため， $N/2+1$ 個目のデータを中心に対称形に $N/2+2\sim N$ 個目の円振動数を定義しておく．
- 複素フーリエ係数の演算も同様に，係数は $N/2+1$ 個目のデータを中心に対称形に格納するが，虚数部は符号を逆転させる．
\begin{equation}
f_k=\frac{k}{N\cdot\Delta t} \qquad \omega_k=2\pi f_k \qquad k=0\sim N/2
\end{equation}
以下にFFTを用いて応答加速度時刻歴を求めるステップを示す．
 |
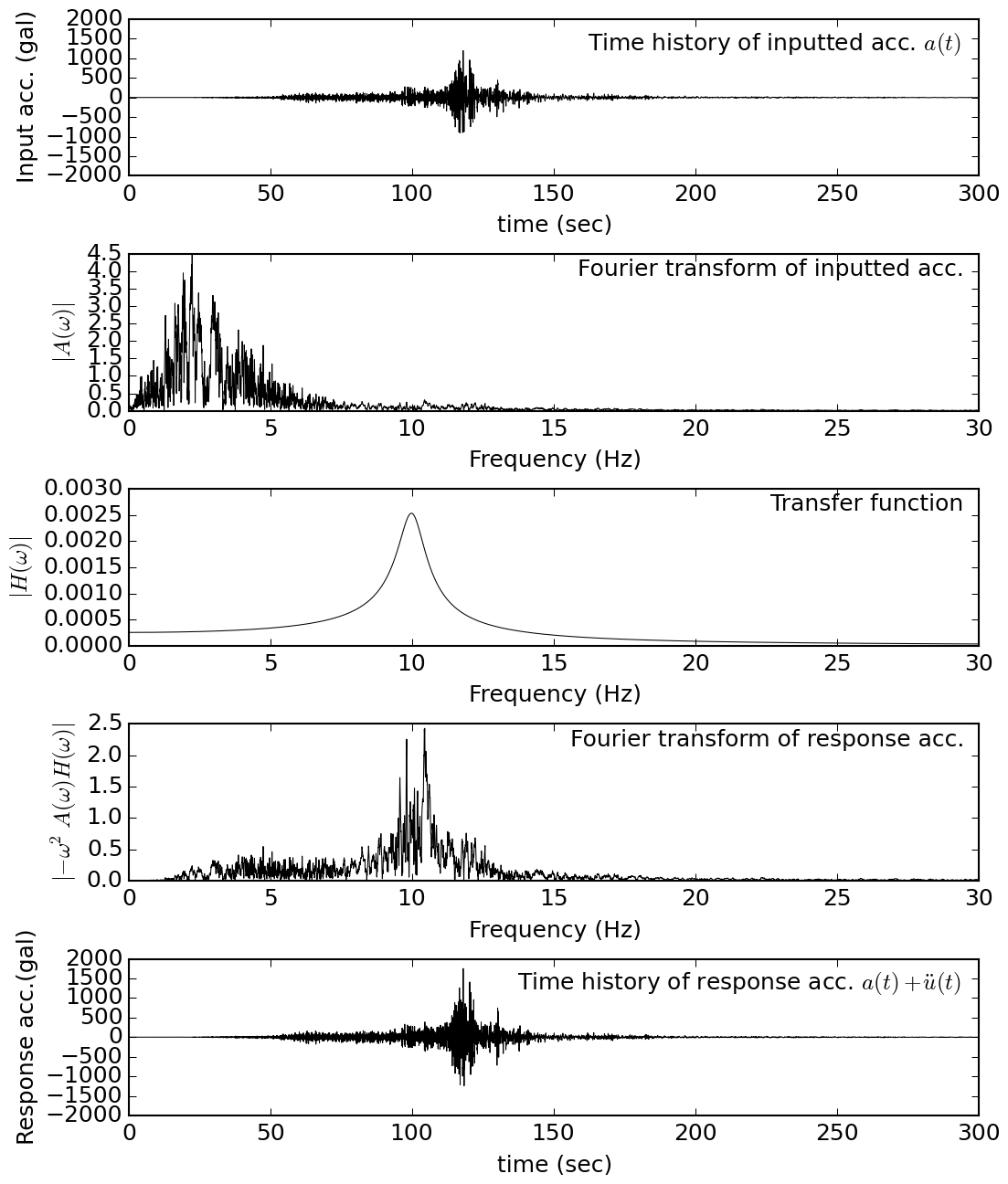| Steps for frequency domain analysis of SDOF (acceleration responce) (damping factor: h=0.05, natural frequency: 10Hz) |
|---|
 |
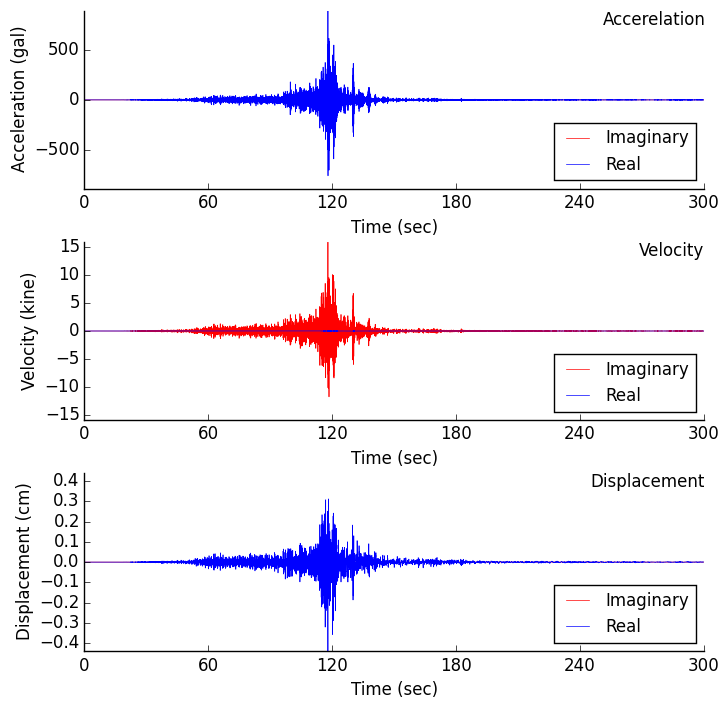| Time histories of Acceleration, Velocity and Displacement |
|---|
上図は，応答波形の時刻歴であるが，加速度および変位の時刻歴はフーリエ逆変換の実数部に格納されるが，速度についてはフーリエ逆変換の虚数部に時刻歴が格納されることに注意を要する．
この積分法を用いて，応答スペクトルを計算した結果を以下に示す．
 |
 |
| Acceleration response spectrum by FFT |
Tripartite response spectrum by FFT |
|---|
地震動解析のためのプログラムソースコード
運動方程式解法，応答スペクトル，フーリエスペクトル
| Filename | Description |
|---|---|
| a_f90.txt | 実行用シェルスクリプト |
| f90_blc.f90 | 加速度データ基線補正 |
| f90_acc_fft.f90 | 運動方程式積分(FFT) |
| f90_acc_nmk.f90 | 運動方程式積分(Newmark法) |
| f90_acc_rng.f90 | 運動方程式積分(Runge-Kutta法) |
| f90_ars_fft.f90 | 加速度応答スペクトル(FFT) |
| f90_ars_nmk.f90 | 加速度応答スペクトル(Newmark法) |
| f90_ars_rng.f90 | 加速度応答スペクトル(Runge-Kutta法) |
| f90_fsp.f90 | Fourierスペクトル |
| f90_eqsp.f90 | 加速度応答スペクトル(大崎氏) |
| dat_acc_TCGH16_EW2.csv | KiKネット地震波(TCGH16_EW2) |
| dat_acc_TCGH16_NS2.csv | KiKネット地震波(TCGH16_NS2) |
| dat_acc_TCGH16_UD2.csv | KiKネット地震波(TCGH16_UD2) |
| inp_acc_ew2.csv | 基線補正後加速度(ew2) |
| inp_acc_ns2.csv | 基線補正後加速度(ns2) |
| inp_acc_ud2.csv | 基線補正後加速度(ud2) |
| py_fig_acc.py | 加速度時刻歴描画 |
| py_fig_spc.py | 加速度応答スペクトル描画 |
| py_fig_tri.py | 3重応答スペクトル描画 |
| py_fig_fsp.py | Fourierスペクトル描画 |
| py_fig_acc_fft.py | FFT法ステップ描画 |
| py_fig_acc_fft_ri.py | FFT法加速度・速度・変位描画 |
| a_gmt_model.txt | 質点モデル描画GMTコマンド |
模擬地震波作成
| Filename | Description |
|---|---|
| a_f90.txt | 実行用シェルスクリプト |
| f90_wave_rand.f90 | 原種波形作成(乱数使用) |
| f90_wave_make.f90 | 模擬地震波作成 |
| inp_kagen-sp.csv | 目標加速度応答スペクトル入力データ事例 |
| inp_ran1.csv | 原種波形(1) |
| inp_ran2.csv | 原種波形(2) |
| inp_ran3.csv | 原種波形(3) |
| acc_ran1.csv | 模擬地震波(1) |
| acc_ran2.csv | 模擬地震波(2) |
| acc_ran3.csv | 模擬地震波(3) |
| a_gmt_spc.txt | 地震波描画GMTコマンド(Control) |
| a_gmt_spc_add.txt | 地震波描画GMTコマンド(Drawing) |
| a_f90_phase.txt | 位相角計算実行用シェルスクリプト |
| f90_wave_phase.f90 | 位相スペクトル |
| inp_test1.csv | 位相スペクトル計算用入力データ事例(原種波形) |
| inp_test2.csv | 位相スペクトル計算用入力データ事例(模擬地震波) |
| a_gmt_phase.txt | 位相角描画GMTコマンド |
| a_gmt_func.txt | 包絡関数描画GMTコマンド |