Stresses in RC members
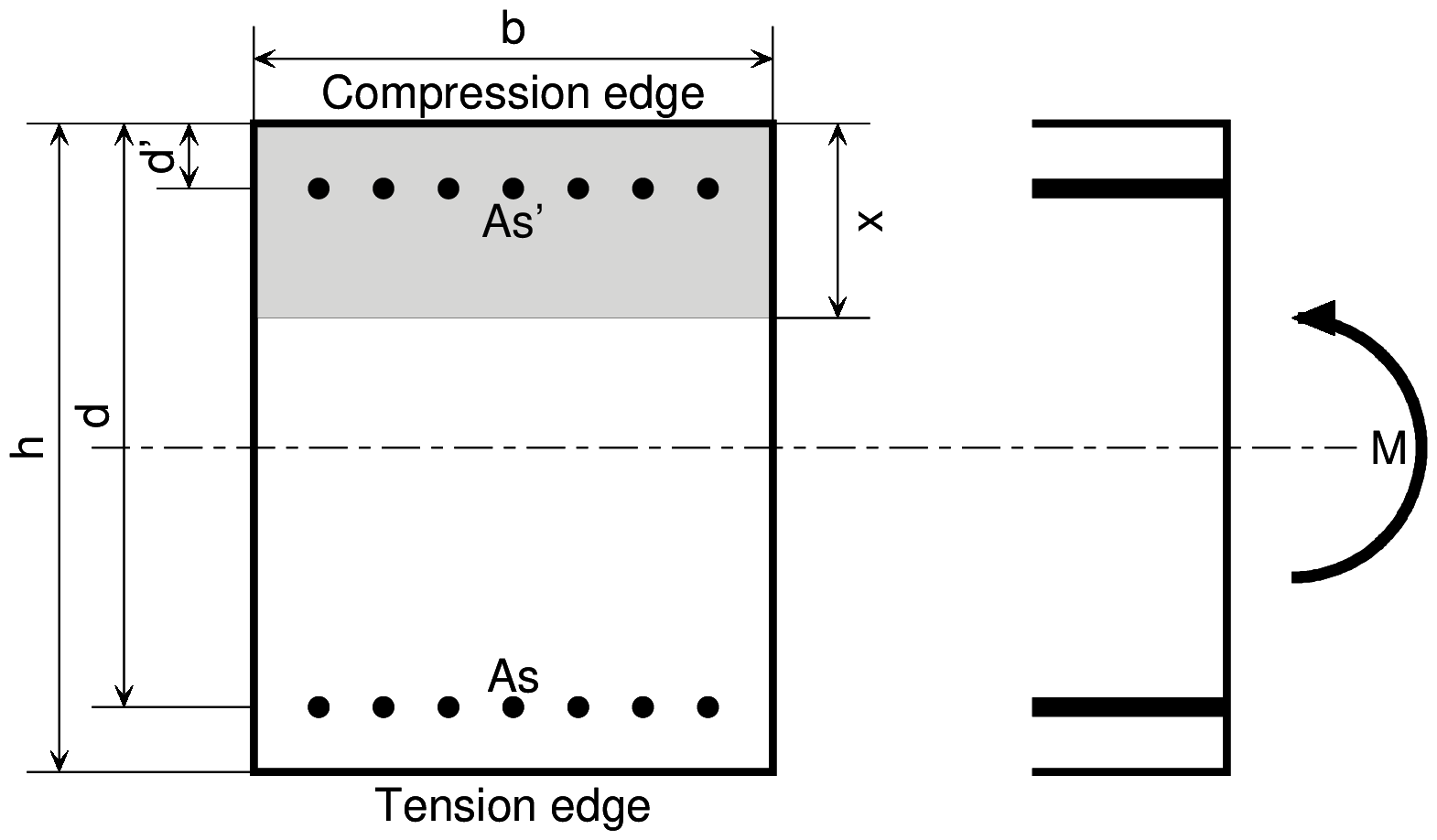
| Model under Bending Moment |
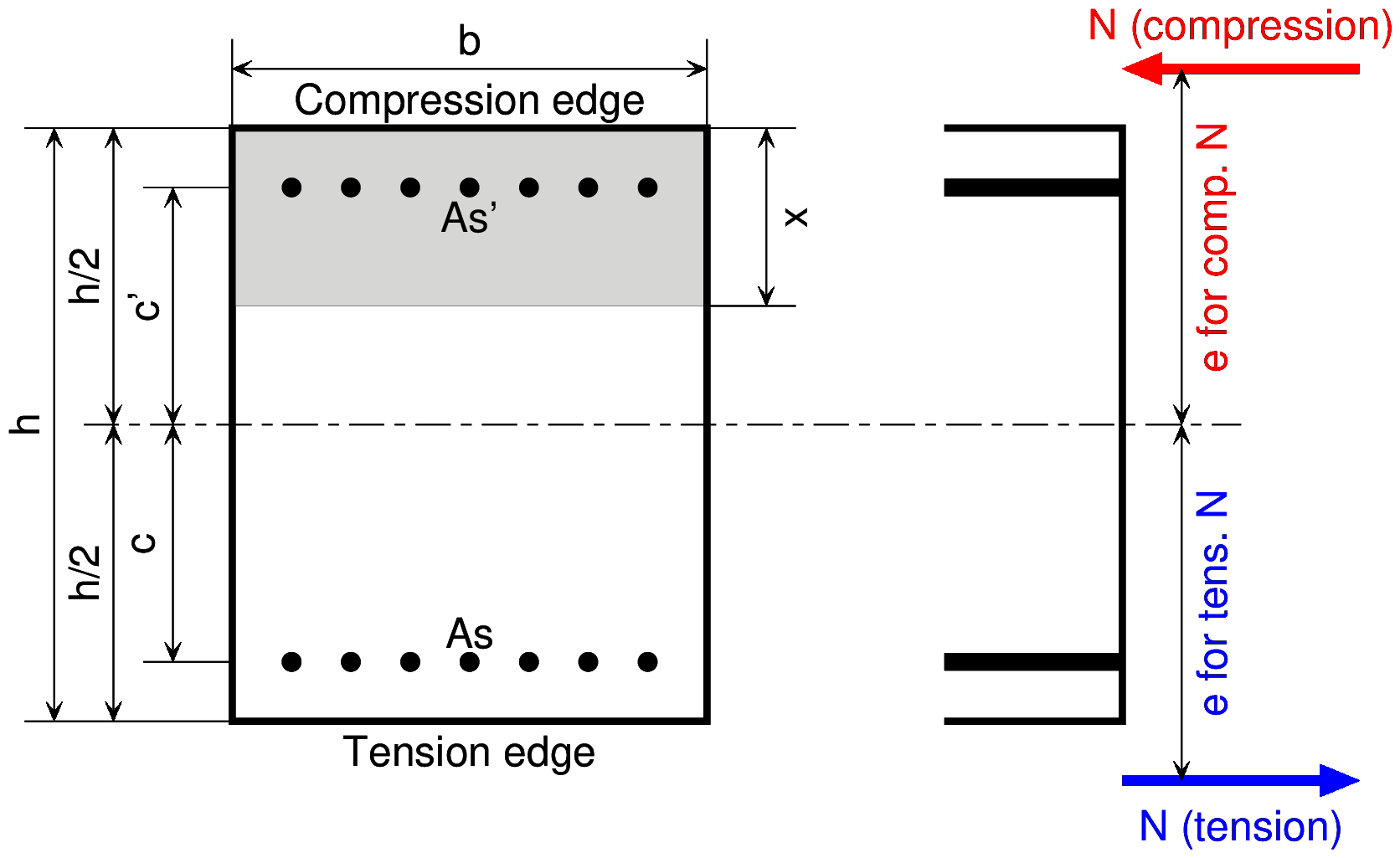
Model under Axial Force & Bending Moment |
|---|---|
 |
 |
| $b$ | Width of rectangular section |
| $h$ | Height of rectangular section |
| $M$ | Bending moment |
| $N$ | Axial force |
| $x$ | Distance from compression edge to neutral axis |
| $\sigma_c$ | Compressive stress of Concrete |
| $\sigma_s$ | Tensile stress of Tensile re-bar |
| $\sigma_s'$ | Compressive stress of Compressive re-bar |
| $n$ | Ratio of elastic moduluses of rebar and concrete (=15) |
| $A_s$ | Total section area of tensile re-bars |
| $A_s'$ | Total section area of compressive rebars |
Single Reinforcement Rectangular Section under Bending Moment
\begin{equation} x=\cfrac{n A_s}{b} \left[-1+\sqrt{1+\cfrac{2 b d}{n A_s}} \right] \end{equation} \begin{equation} \sigma_c=\cfrac{2 M}{b x \left(d-\cfrac{x}{3}\right)} \end{equation} \begin{equation} \sigma_s=\cfrac{M}{A_s \left(d-\cfrac{x}{3}\right)}=n \sigma_c \cfrac{d-x}{x} \end{equation}Double reinforcements rectangular section under bending moment
\begin{equation} x=-n\cfrac{A_s+A_s'}{b}+\sqrt{\left[\cfrac{n (A_s+A_s')}{b}\right]^2+\cfrac{2 n}{b} (d A_s + d' A_s')} \end{equation} \begin{equation} \sigma_c=\cfrac{M}{\cfrac{b x}{2} \left(d-\cfrac{x}{3}\right) + n A_s' \cfrac{x-d'}{x}(d-d')} \end{equation} \begin{equation} \sigma_s=n \sigma_c \cfrac{d-x}{x} \end{equation} \begin{equation} \sigma_s'=n \sigma_c \cfrac{x-d'}{x} \end{equation}Double Reinforcements Rectangular Section under Compressive Axial force and Bending Moment
\begin{equation} e=M/N \end{equation} \begin{equation} x^3-x^2\cdot 3\left(\cfrac{h}{2}-e\right)+x\cdot\cfrac{6n}{b}[A_s (e+c)+A_s' (e-c')]\\ -\cfrac{6n}{b}\left[A_s \left(c+\cfrac{h}{2}\right)(e+c)+A_s' \left(\cfrac{h}{2}-c'\right)(e-c')\right] =0 \end{equation} \begin{equation} \sigma_c=\cfrac{M}{\cfrac{b x}{2}\left(\cfrac{h}{2}-\cfrac{x}{3}\right)+\cfrac{n A_s'}{x} c' \left(c'-\cfrac{h}{2}+x\right)+\cfrac{n A_s}{x} c \left(c+\cfrac{h}{2}-x\right)} \end{equation} \begin{equation} \sigma_s=\cfrac{n \sigma_c}{x} \left(c+\cfrac{h}{2}-x\right) \end{equation} \begin{equation} \sigma_s'=\cfrac{n \sigma_c}{x} \left(c'-\cfrac{h}{2}+x\right) \end{equation}Double Reinforcements Rectangular Section under Tensile Axial force and Bending Moment
\begin{equation} e=M/N \end{equation} \begin{equation} x^3-x^2\cdot 3\left(\cfrac{h}{2}+e\right)-x\cdot\cfrac{6n}{b}[A_s (e-c)+A_s' (e+c')]\\ +\cfrac{6n}{b}\left[A_s \left(c+\cfrac{h}{2}\right)(e-c)+A_s' \left(\cfrac{h}{2}-c'\right)(e+c')\right] =0 \end{equation} \begin{equation} \sigma_c=\cfrac{M}{\cfrac{b x}{2}\left(\cfrac{h}{2}-\cfrac{x}{3}\right)+\cfrac{n A_s'}{x} c' \left(c'-\cfrac{h}{2}+x\right)+\cfrac{n A_s}{x} c \left(c+\cfrac{h}{2}-x\right)} \end{equation} \begin{equation} \sigma_c=\cfrac{N}{\cfrac{n A_s}{x}\left(c+\cfrac{h}{2}-x\right)-\cfrac{n A_s'}{x} \left(c'-\cfrac{h}{2}+x\right)-\cfrac{b x}{2}} \end{equation} \begin{equation} \sigma_s=\cfrac{n \sigma_c}{x} \left(c+\cfrac{h}{2}-x\right) \end{equation} \begin{equation} \sigma_s'=\cfrac{n \sigma_c}{x} \left(c'-\cfrac{h}{2}+x\right) \end{equation}Maximum Shearing Stress of Concrete and Required Section Area of Stirrup
| $S$ | Shearing force |
| $\tau_c$ | Shearing sress of concrete |
| $\tau_{ca}$ | Allowable shearing stress of concrete |
| $\sigma_{sa}$ | Allowable stress of re-bar |
| $V_s$ | Shearing force shared by stirrup |
| $A_v$ | Required section area of stirrup |
Concrete and Re-bar Stresses of Circular Cross Section
| $r$ | Radius of circular cross section |
| $r_s$ | Location of re-bars in radial direction |
| $M$ | Bending moment |
| $N$ | Axial force |
| $\sigma_c$ | Compressive stress of Concrete |
| $\sigma_s$ | Tensile stress of Tensile re-bar |
| $n$ | Ratio of elastic moduluses of rebar and concrete (=15) |
| $A_s$ | Total section area of re-bars |
| $\alpha$ | Location of neutral axis in radian ($0 < \alpha < \pi$) |
Using following equation, $\alpha$ can be calculated by Bisection method.
\begin{equation} \cfrac{e}{r}=\cfrac{\cfrac{\sin 4\alpha}{32}+\cfrac{\pi-\alpha}{8}+\cfrac{\sin^3\alpha\cdot\cos\alpha}{3}+\cfrac{n A_s}{4 r^2}\left(\cfrac{r_s}{r}\right)^2} {\cfrac{\sin^3\alpha}{3}+\cfrac{\sin\alpha\cdot\cos^2\alpha}{2}+\cfrac{(\pi-\alpha)\cos\alpha}{2}+\cfrac{n A_s \cos\alpha}{2 r^2}} \end{equation}After getting $\alpha$, concrete stress and re-bar stress can be calculated using following equations.
\begin{equation} \sigma_c=\cfrac{M (1+\cos\alpha)}{2 r^3 \left\{\cfrac{\sin 4\alpha}{32}+\cfrac{\pi-\alpha}{8}+\cfrac{\sin^3\alpha\cdot\cos\alpha}{3}\right\}+\cfrac{n A_s r_s^2}{2 r}} \end{equation} \begin{equation} \sigma_s=n \sigma_c \cfrac{\cfrac{r_s}{r}-\cos\alpha}{1+\cos\alpha} \end{equation}Checking of $\alpha$ value
\begin{equation} \cos\alpha=\cfrac{n \cfrac{r_s}{r}-\cfrac{\sigma_s}{\sigma_c}}{\cfrac{\sigma_s}{\sigma_c}+n} \end{equation}Shearing stress of concrete and requied section area of shear re-bar will be calculated using a rectangular cross section model with equivalent cross section area to the circular cross section.
NATM支保計算での支保部材の扱い
Stress of Shotcrete
The compressive strength of the shotcrete is a function of the age, and the elastic modulus is also a function of the age. In addition, the stress of the shotcrete may not be equal to its compressive strength. Therefore, stress increment shall be considered to calculate the shotcrete stresses, and it can be expressed using the age variable tt as follow:
\begin{equation} \sigma_{sc}(t+\Delta t)=\sigma_{sc}(t)+E_{sc}(t+\Delta t / 2) \times \frac{\Delta u_{a}}{a} \end{equation}Where, $\Delta u_a$ is the displacement increment in the radial direction during the small time $\Delta t$, and $\Delta u_a / a$ means the strain increment of the shotcrete in the circumferential direction.
Stress of Rockbolt
The stress of the rockbolt σrbσrb can be obtained using following equation.
\begin{equation} \sigma_{rb}=E_{rb} \times \frac{u_a(t)-u_b(t)}{L} \end{equation}Where, $u_a(t)$ is the tunnel surface displacement at shotcrete age $t$ and $u_b(t)$ is the displacement of the end point of the rockbolt at the shotcrete age $t$. $L$ is the length of the rockbolt, and it can be understood that the second term on right side means the elongation of the rockbolt. If the value $\sigma_{rb}$ reachs to the yeild strength, it is set to the yeild strength of the rockbolt.
$u_b(t)$ can be calculated as a function of $u_a(t)$ using following equations.
Elastic state \begin{equation} u_b(t)=u_a(t) \times \frac{a}{a+L} \end{equation}
Plastic state \begin{equation} u_b(t)=\frac{R^2}{a+L} \cdot \frac{1+\nu}{E} (P_0-P_R) \end{equation} \begin{equation} P_r=\frac{2 P_0-q_u}{\zeta+1} \qquad a < R = \sqrt{u_a(t) \cdot a \cdot \frac{E}{1+\nu} \cdot \frac{\zeta+1}{P_0 (\zeta-1)+q_u}} \end{equation}
Where, $R$ is the boundary between the elastic zone and the plastic zone, and $P_R$ is the support pressure at the boundary $R$.
Stress of Steel Rib
The stress of the steel rib $\sigma_{sr}$ can be obtained using following equation.
\begin{equation} \sigma_{sr}=E_{sr} \times \frac{u_a(t)-u_a(0)}{a} \end{equation}Where, $u_a(t)$ is the tunnel surface displacement at shotcrete age $t$ and $u_a(0)$ is the tunnel surface displacement at the shotcrete age 0. It can be understood that the second term on right side means the strain in the circumferential direction. If the value $\sigma_{sr}$ reachs to the yeild strength, it is set to the yeild strength of the steel rib.
岩盤のせん断強度と一軸圧縮強度の関係
Pure shearing strength (cohesion): $c$
Internal friction angle: $\phi$
Unuaxial compressive strength: $\sigma_c$
\begin{equation} \sigma_c=\frac{2 c (1+\sin\phi)}{\cos\phi}=\frac{2 c \cos\phi}{1-\sin\phi} \end{equation}一軸圧縮強度と引張強度より $c$, $\phi$ を求める
Uniaxial compressive strength: $\sigma_c$
Tensile strength: $\sigma_t$
Pure shearing strength (cohesion): $c$
Internal friction angle: $\phi$
\begin{equation} c=\frac{\sigma_c \sigma_t}{(\sigma_c+\sigma_t) \cos\phi} \qquad \phi=\sin^{-1}\left(\frac{\sigma_c-\sigma_t}{\sigma_c+\sigma_t}\right) \end{equation}最小点安全率 (ダム)
ダム分野で使われる最小点安全率計算式. モール円上の点と破壊基準(直線)との鉛直距離. $\sigma - \tau$平面において$\tau$軸に平行な距離)が最小となる時の安全率を求める.
応力表示 \begin{equation} \sigma=\frac{\sigma_1+\sigma_3}{2}+\frac{\sigma_1-\sigma_3}{2}\cos(2\alpha) \end{equation} \begin{equation} \tau=\frac{\sigma_1-\sigma_3}{2}\sin(2\alpha) \end{equation}
安全率 \begin{equation} SF=\frac{c+\sigma \tan\phi}{\tau}=\frac{c+\left[\frac{\sigma_1+\sigma_3}{2}+\frac{\sigma_1-\sigma_3}{2}\cos(2\alpha)\right]\tan\phi}{\frac{\sigma_1-\sigma_3}{2}\sin(2\alpha)} \end{equation}
$\alpha$の関数である安全率$SF$を最小にする条件
\begin{equation} \frac{\partial(SF)}{\partial\alpha}=0 \end{equation}より,
\begin{equation} \cos(2\alpha)=\frac{-\frac{\sigma_1-\sigma_3}{2}\tan\phi}{c+\frac{\sigma_1+\sigma_3}{2}\tan\phi} \end{equation}上記$\alpha$を用いることにより,最小点安全率$SF_{min}$を求めることができる.
点安全率計算式 (岩盤・トンネル)
安全率計算のサブルーチンを載せておく. せん断と引張の双方を考慮.せん断破壊式はモールクーロン.
式はまわりくどいようだが,やっていることは以下の通り.
せん断安全率:平均応力から破壊基準線への垂線の長さとモール円の半径の比
引張安全率:平均応力から引張強度までの距離と第一主応力から引張強度までの距離の比
double CALSF(double ps1,double ps2,double cc,double fa,double st)
{
/*安全率計算*/
double D1,D2,dd1,dd2,SF1,SF2,SF;
double factL=1.0e10; /*安全率無限大の表示*/
/* ps1 : 第一主応力 */
/* ps2 : 第二主応力 */
/* cc : 純せん断強度 */
/* fa : 内部摩擦角 */
/* st : 引張強度 */
D1=(cc-0.5*(ps1+ps2)*tan(fa/180.0*M_PI))*cos(fa/180.0*M_PI);
dd1=D1-0.5*(ps1-ps2);
D2=st-0.5*(ps1+ps2);
dd2=st-ps1;
/*ps1=ps2の場合D=ddとなり安全率無限大となる*/
if(ps1==ps2){
if(0.0<cc-ps1*tan(fa/180.0*M_PI)){SF=factL;}else{SF1=0.0;}
if(ps1<=0.0){SF2=factL;}else{SF2=st/ps1;}
}else{
SF1=D1/(D1-dd1);
SF2=D2/(D2-dd2);
}
if(SF1<=SF2){SF=SF1;}else{SF=SF2;}
return SF;
}
数式表示事例
Matrix
| matrix | pmatrix | bmatrix | Bmatrix | vmatrix | Vmatrix |
| $\begin{matrix} a & b \\ c & d \end{matrix}$ | $\begin{pmatrix}a & b \\ c & d \end{pmatrix}$ | $\begin{bmatrix}a & b \\ c & d \end{bmatrix}$ | $\begin{Bmatrix}a & b \\ c & d \end{Bmatrix}$ | $\begin{vmatrix}a & b \\ c & d \end{vmatrix}$ | $\begin{Vmatrix}a & b \\ c & d \end{Vmatrix}$ |
Divergence theorem
This theorem is known as Gauss's theorem or Ostrogradsky's theorem.
\begin{equation} \iiint_V\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right)dx dy dz =\iint_S(P dy dz+Q dz dx+R dx dy) \end{equation}Fourier series
Fourier series with period $2\ell$ is shown below. $a_0$, $a_n$ and $b_n$ are Fourier coefficients.
\begin{align} f(x)=&\frac{a_0}{2}+\sum_{n=1}^{+\infty}\left(a_n\cos\frac{n\pi x}{\ell}+b_n\sin\frac{n\pi x}{\ell}\right) \\ &a_0=\frac{1}{\ell}\int_{-\ell}^{\ell}f(x) dx \\ &a_n=\frac{1}{\ell}\int_{-\ell}^{\ell}f(x)\cos\frac{n\pi x}{\ell}dx \qquad (n=1,2,3, \cdots) \\ &b_n=\frac{1}{\ell}\int_{-\ell}^{\ell}f(x)\sin\frac{n\pi x}{\ell}dx \qquad (n=1,2,3, \cdots) \end{align}
Maclaurin expansion
\begin{equation} f(x)=f(0)+\frac{f'(0)}{1!}x+\frac{f''(0)}{2!}x^2+\cdots+\frac{f^{(n-1)}}{(n-1)!}x^{n-1}+\frac{f^{(n)}(\theta x)}{n!}x^n \qquad (0 < \theta < 1) \end{equation} \begin{align} &e^x=1+\frac{x}{1!}+\cdots+\frac{x^{n-1}}{(n-1)!}+\frac{e^{\theta x}}{n!}x^n \qquad (0<\theta<1) \\ &e\doteqdot 1+\frac{1}{1!}+\frac{1}{2!}+\cdots+\frac{1}{(n-1)!} \end{align}Definition of $e$ (Napier's constant)
\begin{equation} \lim_{n\to\pm\infty}\left(1+\frac{1}{x}\right)^x=e \end{equation}Differentiation
\begin{align} &h(x)=f(x)\pm g(x) & \to \qquad & h'(x)=f'(x)\pm g'(x) \\ &h(x)=f(x)\cdot g(x) & \to \qquad & h'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x) \\ &h(x)=\frac{f(x)}{g(x)} & \to \qquad & h'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{g(x)^2} \end{align}De Moivre's formula
\begin{equation} (\cos\phi+i\cdot\sin\phi)^n=\cos(n\phi)+i\cdot\sin(n\phi) \end{equation}Euler's formula
\begin{equation} e^{i z}=\cos z+i\cdot\sin z \end{equation}Hyperbolic function
\begin{equation} \cosh z=\frac{e^z+e^{-z}}{2} \qquad \sinh z=\frac{e^z-e^{-z}}{2} \end{equation}Addition theorem of Trigonometric function
\begin{align} \sin(\alpha+\beta)=&\sin\alpha\cdot\cos\beta+\cos\alpha\cdot\sin\beta \\ \cos(\alpha+\beta)=&\cos\alpha\cdot\cos\beta-\sin\alpha\cdot\sin\beta \end{align}Straight line connecting two points $(x_1,y_1)$ and $(x_2,y_2)$
\begin{equation} y=a\cdot x+b \end{equation} \begin{equation} a=\frac{y_2-y_1}{x_2-x_1} \qquad \qquad b=\frac{x_2\cdot y_1-x_1\cdot y_2}{x_2-x_1} \end{equation}Regression line with data quantity $n$
\begin{equation} y=a\cdot x+b \end{equation} \begin{equation} a=\frac{n \sum xy-\sum x\cdot\sum y}{n \sum x^2-(\sum x)^2} \qquad \qquad b=\frac{\sum x^2\cdot \sum y-\sum x\cdot\sum xy}{n \sum x^2-(\sum x)^2} \end{equation} \begin{equation} r=\frac{n \sum xy-\sum x\cdot\sum y}{\sqrt{[n \sum x^2-(\sum x)^2]\cdot [n \sum y^2-(\sum y)^2]}} \end{equation}Average, Standard deviation
\begin{align} x_m=\frac{\sum x}{n} \qquad \sigma_x=\sqrt{\frac{1}{n-1}\cdot\sum(x_i-x_m)^2} \end{align}Two-dimensional normal distribution
Probability density function
\begin{equation} \begin{cases} \quad f(x,y)=\cfrac{1}{2\pi\cdot\sigma_x\cdot\sigma_y\cdot\sqrt{1-\rho^2}}\cdot\exp\left(-\cfrac{c^2}{2}\right) \\ \quad \\ \quad c^2=\cfrac{1}{1-\rho^2}\left\{\cfrac{(x-x_m)^2}{\sigma_x{}^2}+\cfrac{(y-y_m)^2}{\sigma_y{}^2}-\cfrac{2\rho(x-x_m)(y-y_m)}{\sigma_x\sigma_y}\right\} \end{cases} \end{equation}$x_m$, $y_m$: average
$\sigma_x$, $\sigma_y$: standard deviation
$\rho$: correlation coefficient
